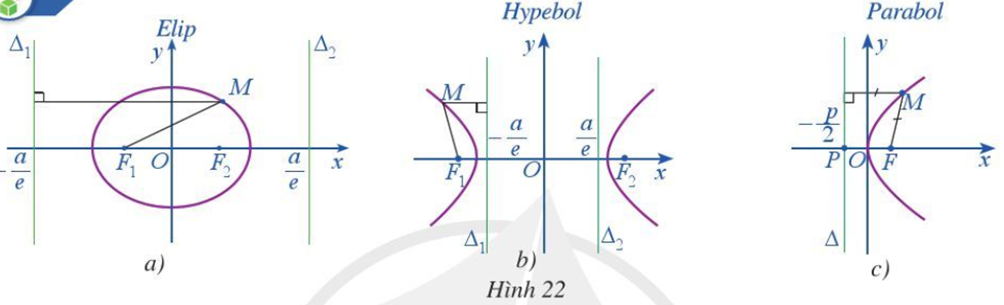
Sao Diêm Vương chuyển động xung quanh Mặt Trời theo quỹ đạo là một đường elip có một trong hai tiêu điểm là tâm của Mặt Trời. Biết elip này có bán trục lớn a ≈ 5,906 . 106 km và tâm sai e ≈ 0,249. (Nguồn: https://vi.wikipedia.org)
Tìm khoảng cách nhỏ nhất (gần đúng) giữa Sao Diêm Vương và Mặt Trời.
Sao Diêm Vương chuyển động xung quanh Mặt Trời theo quỹ đạo là một đường elip có một trong hai tiêu điểm là tâm của Mặt Trời. Biết elip này có bán trục lớn a ≈ 5,906 . 106 km và tâm sai e ≈ 0,249. (Nguồn: https://vi.wikipedia.org)
Tìm khoảng cách nhỏ nhất (gần đúng) giữa Sao Diêm Vương và Mặt Trời.
Câu hỏi trong đề: Bài tập Chuyên đề Ba đường Conic có đáp án !!
Quảng cáo
Trả lời:
Chọn hệ trục toạ độ sao cho Mặt Trời trùng với tiêu điểm F1 của elip.
Khi đó elip có phương trình là (a > b > 0).
Theo đề bài, ta có: elip này có bán trục lớn a ≈ 5,906 . 106 km và tâm sai e ≈ 0,249
Giả sử Sao Diêm Vương có toạ độ là M(x; y).
Khi đó khoảng cách giữa Sao Diêm Vương và Mặt Trời là: MF1 = a + ex.
Vì x ≥ –a nên MF1 ≥ a – ea ≈ 5,906 . 106 – 0,249 . 5,906 . 106 = 4435406 (km).
Vậy khoảng cách nhỏ nhất giữa Sao Diêm Vương và Mặt Trời xấp xỉ 4435406 km.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: 2p = 2
Vậy tiêu điểm của parabol là và đường chuẩn của parabol là
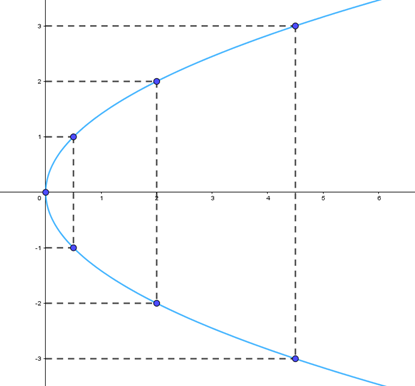
Vẽ parabol:
Bước 1. Lập bảng giá trị
|
x |
0 |
0,5 |
0,5 |
2 |
2 |
4,5 |
4,5 |
|
y |
0 |
–1 |
1 |
–2 |
2 |
–3 |
3 |
Chú ý rằng ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau.
Bước 2. Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị.
Bước 3. Vẽ parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2.
Lời giải
Chọn hệ trục toạ độ sao cho tâm Trái Đất trùng với tiêu điểm F1 của elip.
Khi đó elip có phương trình là (a > b > 0).
Theo đề bài, ta có: vệ tinh cách bề mặt Trái Đất gần nhất là 583 dặm và xa nhất là 1342 dặm, mà bán kính của Trái Đất xấp xỉ 4000 dặm nên vệ tinh cách tâm Trái Đất gần nhất là 583 + 4000 = 4583 dặm và xa nhất là 1342 + 4000 = 5342 dặm.
Giả sử vệ tinh có toạ độ là M(x; y).
Khi đó khoảng cách từ vệ tinh đến tâm Trái Đất là: MF1 = a + ![]() x.
x.
Vì –a ≤ x ≤ a nên a – c ≤ MF1 ≤ a + c.
Vậy khoảng cách nhỏ nhất và lớn nhất từ vệ tinh đến tâm Trái Đất lần lượt là a – c và a + c.
Vậy tâm sai của quỹ đạo này xấp xỉ 0,076.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.