Một nhóm gồm 3 học sinh lớp 10, 3 học sinh lớp 11 và 3 học sinh lớp 12 được xếp ngồi vào một hàng có 9 ghế, mỗi học sinh ngồi 1 ghế. Tính xác suất để 3 học sinh lớp 10 không ngồi 3 ghế liền nhau.
Quảng cáo
Trả lời:
Chọn D
Nhóm có tất cả 9 học sinh nên số cách xếp 9 học sinh này ngồi vào một hàng có 9 ghế là 9! = 362880(cách).
Vậy số phần tử không gian mẫu là = 362880
Đặt biến cố A: “ 3 học sinh lớp không ngồi ghế liền nhau”.
Giả sử học sinh lớp 10 ngồi 3 ghế liền nhau. Ta xem 3 học sinh này là một nhóm
+/ Xếp X và 6 bạn còn lại vào ghế có 7! cách xếp.
+/ Ứng với mỗi cách xếp ở trên, có 3! cách xếp các bạn trong nhóm X.
Vậy theo quy tắc nhân ta có số cách xếp là: 7!.3! = 30240 (cách).
Suy ra số cách xếp để học sinh lớp không ngồi cạnh nhau là (cách) .
Vậy xác suất để học sinh lớp 10 không ngồi cạnh nhau là 362880 - 30240 = 332640 (cách)
=> n(A) = 332640
Vậy xác suất để học sinh lớp 10 không ngồi cạnh nhau là
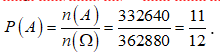
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn A
Số phần tử không gian mẫu: ![]()
TH1: Nếu a = 2
b = 0 ![]() có 4 cách;d có 4 cách.
có 4 cách;d có 4 cách.
Vậy có 16 số.
![]() có 5 cách;c có 5 cách; d có 4 cách.
có 5 cách;c có 5 cách; d có 4 cách.
Vậy có 100 số.
TH2: Nếu ![]() có 3 cách; b có 6 cách; c có 5 cách; d có 4 cách.
có 3 cách; b có 6 cách; c có 5 cách; d có 4 cách.
Vậy có 360 số.
TH3: Nếu a = 9
b = 0; ![]() có 5 cách; d có 4 cách.
có 5 cách; d có 4 cách.
Vậy có 20 số.
Kết luận: ![]() số
số

Lời giải
Chọn D
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố: “cặp sinh đôi ngồi cạnh nhau và nam nữ không ngồi đối diện nhau”.
Ta tính n() như sau:
Đánh số các ghế ngồi của 8 học sinh như hình vẽ sau:
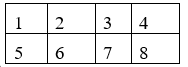
- Để xếp cho cặp sinh đôi ngồi cạnh nhau có 6 cách.
- Mỗi cách như vậy có cách đổi chỗ.
- Với mỗi cách xếp cặp sinh đôi, ví dụ: Cặp sinh đôi ở vị trí 1 và 2.
Do nam nữ không ngồi đối diện nên:
+ Vị trí 5 và 6 đều có 3 cách.
+ Vị trí 3 có 4 cách, vị trí 7 có 1 cách.
+ Vị trí 4 có 2 cách, vị trí 8 có 1 cách.
Suy ra n(A) = 6.2.3.3.4.1.2.1 = 864
![]()
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.