299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1)
56 người thi tuần này 5.0 25.4 K lượt thi 40 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 7 (có lời giải) - Đề 1
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 3
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 2
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 1
Đề kiểm tra Bài tập cuối chương 6 (có lời giải) - Đề 3
Danh sách câu hỏi:
Câu 1
A. 90.
B. 5.
C. 180.
D. 10 .
Lời giải
Chọn B
Ta có: 20 = 1 + 19 = 3 + 17 = 5 + 15 = 7 + 13 mà vòng đeo tay gồm 20 hạt giống nhau nên có 5 cách cắt chiếc vòng đó thành 2 phần mà số hạt ở mỗi phần đều là số lẻ.
Lời giải
Chọn C
Lời giải
Chọn C
Theo quy tắc nhân ta có số cách là mn
Lời giải
Chọn B
Lấy ra 3 chữ số từ 9 chữ số và sắp xếp 3 chữ số đó theo thứ tự, mỗi cách sắp xếp tạo nên 1 số có 3 chữ số khác nhau. Như vậy, có số cần tìm.
* Nhận xét: Mục đích bài toán là phân biệt hai khái niệm: Chỉnh hợp và tổ hợp. Học sinh có thể giải bài này bằng phương pháp nhân: 9.8.7, và so sánh với 4 đáp án. Hai chỉnh hợp khác nhau thì có thể khác nhau về phần tử hoặc khác nhau về thứ tự các phần tử. Hai tổ hợp khác nhau thì khác nhau về phần tử.
*Lý thuyết Chỉnh hợp
- Cho tập hợp A có n phần tử và cho số nguyên k, (1 k n). Khi lấy k phần tử của A và sắp xếp chúng theo một thứ tự, ta được một chỉnh hợp chập k của n phần tử của A (gọi tắt là một chỉnh hợp n chập k của A).
- Số các chỉnh hợp chập k của một tập hợp có n phần tử là: 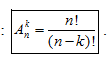
- Một số qui ước: ![]()
*Lý thuyết Tổ hợp
- Cho tập hợp A có n phần tử và cho số nguyên k, (1 k n). Mỗi tập hợp con của A có phần tử được gọi là một tổ hợp chập k của n phần tử của A.
- Số các chỉnh hợp chập k của một tập hợp có n phần tử là : 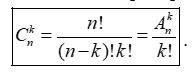
- Một số quy ước: ![]() với qui ước này ta có
với qui ước này ta có 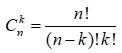 đúng với số nguyên dương k, thỏa 0 k n
đúng với số nguyên dương k, thỏa 0 k n
PT 14.1. Chọn B
TH1 ![]()
TH2: ![]() vì
vì ![]()
Như vậy, có ![]() số cần tìm
số cần tìm
PT 14.2.
Chọn C
Mỗi tập con có 3 phần tử thuộc tập {1,2,...,9} xác định duy nhất một số có 3 chữ số tăng dần từ trái qua phải (đảm bảo chữ số đầu tiên khác 0).
Mỗi tập con có 3 phần tử thuộc tập {0,1,2....,9} xác định duy nhất một số có 3 chữ số giảm dần từ trái qua phải.
Như vậy, có ![]() số cần tìm.
số cần tìm.
Câu 5
A. 120
B. 231
C. 210
D. 22
Lời giải
Chọn A
Số cách chọn một bạn nam là 12 cách.
Số cách chọn một bạn nữ là 10 cách
Vậy số cách chọn hai bạn trực nhật có cả nam và nữ là 12.10 = 120 (cách)
Câu 6
A. 10
B. 90.
C. 45.
D. 24.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. 720
B. 600
C. 625
D. 240
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. 234.
B. 132.
C. 243.
D. 432.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. T = 11003984
B. T = 36011952
C. T = 12003984
D. T = 18005967
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. 8 cách.
B. 12 cách.
C. 24 cách.
D. 4 cách.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
A. 24
B. 4
C. 12
D. 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
A. Chỉnh hợp chập k của n phần tử.
B. Số tổ hợp chập k của n phần tử.
C. Tổ hợp chập k của n phần tử.
D. Số chỉnh hợp chập k của n phần tử.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
A. 216
B. 120
C. 504
D. 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 36
A. 720.
B. 120.
C. 59049.
D. 3628800.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.