21 câu Dạng 1: Quy nạp toán học có đáp án
41 người thi tuần này 4.6 6.5 K lượt thi 21 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải

Lời giải


Lời giải

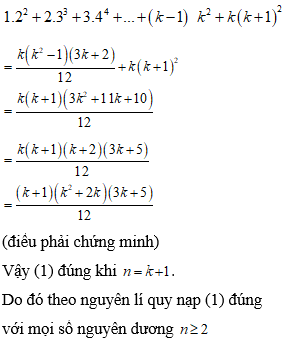
Lời giải

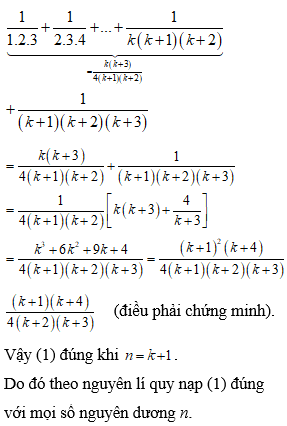
Lời giải


Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. Sai từ bước 1
B. Sai từ bước 3
C. Sai từ bước 2
D. Lập luận hoàn toàn đúng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. Sai từ bước 1
B. Sai từ bước 3
C. Sai từ bước 2
D. Lập luận hoàn toàn đúng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. Sai từ bước 1
B. Sai từ bước 3
C. Sai từ bước 2
D. Lập luận hoàn toàn đúng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. Mọi số nguyên bé hơn k đều thuộc A.
B. Mọi số nguyên dương đều thuộc A.
C. Mọi số nguyên dương lớn hơn hoặc bằng k đều thuộc A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. Chỉ có bước 2 đúng.
B. Cả hai bước đều đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.