Cho phương trình \(\sqrt {26{x^2} - 63x + 38} = 5x - 6\).

a) Bình phương hai vế và giải phương trình nhận được.

b) Thử lại các giá trị x tìm được ở câu a có thỏa mãn phương trình hay không?

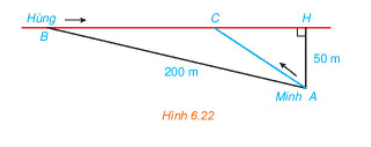
Đổi: 200 m = 0,2 km, 50 m = 0,05 km.

Đặt CH = x (km) (x > 0).

Xét tam giác CHA vuông tại H, theo định lí Pythagore ta có:

CA² = HA² + HC² = (0,05)² + x² = 0,0025 + x²

Suy ra CA = $\sqrt{\mathrm{0,0025}+x^2}$ hay quãng đường di chuyển của Minh từ vị trí A đến điểm gặp nhau C dài $\sqrt{\mathrm{0,0025}+x^2}$ km.

Vận tốc đi bộ của Minh là 5 km/h nên thời gian di chuyển của Minh từ vị trí A đến điểm gặp nhau C là: $\frac{\sqrt{\mathrm{0,0025}+x^2}}{5}$ (giờ).

Xét tam giác HAB vuông tại H, theo định lí Pythagore ta có:

AB² = HB² + HA² ⇔ HB² = AB² – HA² = (0,2)² – (0,05)² = 0,0375

Suy ra HB = $\frac{\sqrt{15}}{20}$.

Ta có: BC + CH = HB ⇔ BC = HB – CH = $\frac{\sqrt{15}}{20}-x$.

Do đó quãng đường di chuyển của Hùng từ B đến điểm gặp nhau C dài $\frac{\sqrt{15}}{20}-x$ km.

Vận tốc đạp xe của Hùng là 15 km/h nên thời gian di chuyển của Hùng từ B đến điểm gặp nhau là: $\frac{\frac{\sqrt{15}}{20}-x}{15}=\frac{\sqrt{15}-20x}{300}$ (giờ).

Để hai bạn gặp nhau mà không bạn nào phải chờ người kia thì thời gian di chuyển từ vị trí A đến C của Minh phải bằng thời gian di chuyển từ vị trí B đến C của Hùng.

Khi đó ta có phương trình: $\frac{\sqrt{\mathrm{0,0025}+x^2}}{5}=\frac{\sqrt{15}-20x}{300}$    (1).

Giải phương trình (1) ta có:

(1) $\iff 60\sqrt{\mathrm{0,0025}+x^2}=\sqrt{15}-20x$

Bình phương hai vế của phương trình trên ta được:

3600.(0,0025 + x²) = 15 – 40$\sqrt{15}$x + 400x²

⇔ 3200x² + 40$\sqrt{15}$x – 6 = 0

⇔ x = $\frac{-\sqrt{15}-3\sqrt{7}}{160}$ hoặc x = $\frac{-\sqrt{15}+3\sqrt{7}}{160}$

Thay lần lượt các giá trị này vào phương trình (1) ta thấy cả hai giá trị đều thỏa mãn.

Lại có điều kiện của x là x > 0 nên ta chọn x = $\frac{-\sqrt{15}+3\sqrt{7}}{160}$≈ 0,0254.

Suy ra BC = BH – CH ≈ $\frac{\sqrt{15}}{20}-\mathrm{0,0254}\approx \mathrm{0,1682}$ km = 168,2 m.

Vậy vị trí C thỏa mãn yêu cầu đề bài là điểm cách B khoảng 168,2 m.

Hướng dẫn giải

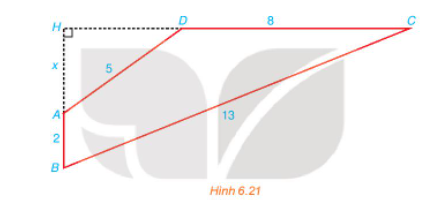
Đặt AH = x, x > 0.

Xét tam giác AHD vuông tại H, theo định lí Pythagore ta có:

AD² = AH² + HD² ⇔ HD² = AD² – AH² = 5² – x² = 25 – x²

Suy ra HD = \(\sqrt {25 - {x^2}} \).

Ta có HC = HD + DC = \(\sqrt {25 - {x^2}} + 8\).

HB = AH + AB = x + 2

Xét tam giác HBC vuông tại H, theo định lí Pythagore ta có:

BC² = HB² + HC²

⇔ 13² = (x + 2)² + \({\left( {\sqrt {25 - {x^2}} + 8} \right)^2}\)

⇔ x² + 4x + 4 + 25 – x² + 16\(\sqrt {25 - {x^2}} \)+ 64 – 169 = 0

⇔ 16\(\sqrt {25 - {x^2}} \) = – 4x + 76

⇔ 4\(\sqrt {25 - {x^2}} \) = – x + 19

Để tính x, ta cần giải phương trình: 4\(\sqrt {25 - {x^2}} \) = – x + 19 (1).

Bình phương hai vế của phương trình (1) ta được:

16.(25 – x²) = x² – 38x + 361

⇔ 17x² – 38x – 39 = 0  

⇔ x = 3 hoặc x = \( - \frac{{13}}{{17}}\).

Thay lần lượt các giá trị trên vào phương trình (1), ta thấy hai giá trị x = 3 và x = \( - \frac{{13}}{{17}}\) đều thỏa mãn.

Vì điều kiện của x là x > 0 nên ta chọn x = 3.

Do đó ta tính được AH = 3.

Suy ra HD = \(\sqrt {25 - {3^2}} = 4\).

HC = 4 + 8 = 12

HB = 3 + 2 = 5

Diện tích tam giác HAD là S₁ = \(\frac{1}{2}\)HA . HD = \(\frac{1}{2}\). 3 . 4 = 6.

Diện tích tam giác HBC là S₂ = \(\frac{1}{2}\)HB . HC = \(\frac{1}{2}\) . 5 . 12 = 30.

Vậy diện tích tứ giác ABCD là S = S₂ – S₁ = 30 – 6 = 24.