Câu hỏi:
28/06/2022 209
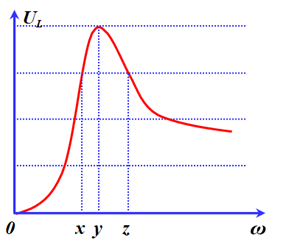
Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi vào hai đầu đoạn mạch AB mắc nối tiếp gồm cuộn dây thuần cảm có độ tự cảm L, điện trở R và tụ điện có điện dung C. Tần số góc ω của điện áp là thay đổi được. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng trên L theo giá trị tần số góc ω. Lần lượt cho ω bằng x, y và z thì mạch AB tiêu thụ công suất lần lượt là P1, P2 và P3. Biểu thức nào sau đây đúng?
Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi vào hai đầu đoạn mạch AB mắc nối tiếp gồm cuộn dây thuần cảm có độ tự cảm L, điện trở R và tụ điện có điện dung C. Tần số góc ω của điện áp là thay đổi được. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng trên L theo giá trị tần số góc ω. Lần lượt cho ω bằng x, y và z thì mạch AB tiêu thụ công suất lần lượt là P1, P2 và P3. Biểu thức nào sau đây đúng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Phương pháp giải:
Sử dụng kĩ năng đọc đồ thị
Điện áp ULmax khi tần số có giá trị ω2
Hai tần số ω1, ω3 cho cùng giá trị điện áp \({U_L}:\frac{1}{{{\omega _1}^2}} + \frac{1}{{{\omega _3}^2}} = \frac{2}{{{\omega _2}^2}}\)
Độ lệch pha giữa điện áp và cường độ dòng điện: \(\cos \varphi = \frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Điện áp hiệu dụng giữa hai đầu cuộn dây: \({U_L} = \frac{{U.{Z_L}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Công suất tiêu thụ: \(P = \frac{{{U^2}{{\cos }^2}\varphi }}{R}\)
Giải chi tiết:
Điện áp hiệu dụng giữa hai đầu cuộn dây là:
\({U_L} = \frac{{U.{Z_L}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{U.{Z_L}}}{R}.\frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{U.{Z_L}.cos\varphi }}{R}\)
Với tần số ω1 = x; ω2 = y và ω3 = z, ta có: \(\frac{1}{{{\omega _1}^2}} + \frac{1}{{{\omega _3}^2}} = \frac{2}{{{\omega _2}^2}}\)
Từ đồ thị ta thấy: \({U_{L1}} = {U_{L3}} = \frac{3}{4}{U_{L2}} = \frac{3}{4}{U_{L\max }}\)
\( \Rightarrow \frac{{U.{Z_{L1}}\cos {\varphi _1}}}{R} = \frac{{U.{Z_{L3}}\cos {\varphi _3}}}{R} = \frac{3}{4}\frac{{U.{Z_{L2}}\cos {\varphi _2}}}{R}\)
\( \Rightarrow {\omega _1}^2{\cos ^2}{\varphi _1} = {\omega _3}^2{\cos ^2}{\varphi _3} = \frac{9}{{16}}{\omega _2}^2{\cos ^2}{\varphi _2}\)
\[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} = \frac{9}{{16}}\frac{{{\omega ^2}}}{{{\omega _1}^2}}}\\{\frac{{{{\cos }^2}{\varphi _2}}}{{{{\cos }^2}\varphi }} = \frac{9}{{16}}\frac{{{\omega ^2}}}{{{\omega _2}^2}}}\end{array}} \right.\]\( \Rightarrow \frac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} + \frac{{{{\cos }^2}{\varphi _3}}}{{{{\cos }^2}{\varphi _2}}} = \frac{9}{{16}}{\omega ^2}.\left( {\frac{1}{{{\omega _1}^2}} + \frac{1}{{{\omega _3}^2}}} \right)\)
\( \Rightarrow \frac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} + \frac{{{{\cos }^2}{\varphi _2}}}{{{{\cos }^2}{\varphi _2}}} = \frac{9}{{16}}{\omega _2}^2.\frac{2}{{{\omega _2}^2}} = \frac{9}{8}{\mkern 1mu} {\mkern 1mu} \left( 1 \right)\)
Công suất tiêu thụ của mạch điện là: \(P = \frac{{{U^2}{{\cos }^2}\varphi }}{R} \Rightarrow P\~{\cos ^2}\varphi \)
Từ (1) ta có: \(\frac{{{P_1}}}{{{P_2}}} + \frac{{{P_3}}}{{{P_2}}} = \frac{9}{8} \Rightarrow \frac{{{P_1} + {P_3}}}{9} = \frac{{{P_2}}}{8}\).
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án C
Phương pháp giải:
Tính \(y'\) và tìm điều kiện để \(y' \ge 0,\forall x \in \mathbb{R}\).
Chú ý: Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\).
Khi đó: \(f\left( x \right) \ge 0,\forall x \in R \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 0}\\{\Delta \le 0}\end{array}} \right.\)
\(f\left( x \right) \le 0,\forall x \in R \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a < 0}\\{\Delta \le 0}\end{array}} \right.\).
Giải chi tiết:
Ta có : \(y' = {x^2} + 4mx + 8\)
Hàm số đồng biến trên \(\left( { - \infty ; + \infty } \right)\)
\( \Leftrightarrow y' \ge 0,\forall x \in \mathbb{R} \Leftrightarrow {x^2} + 4mx + 8 \ge 0,\forall x \in \mathbb{R}\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1 > 0}\\{\Delta ' = 4{m^2} - 8 \le 0}\end{array}} \right. \Leftrightarrow {m^2} \le 2 \Leftrightarrow - \sqrt 2 \le m \le \sqrt 2 \)
Mà \(m \in \mathbb{Z}\) nên \(m \in \left\{ { - 1;0;1} \right\}\).
Vậy có 3 giá trị thỏa mãn.
Lời giải
Đáp án B
Phương pháp giải:
Gọi x là số mol KAl(SO4)2.12H2O kết tinh.
Vì nhiệt độ không đổi nên độ tan cũng không đổi do đó nồng độ dung dịch bão hòa không đổi.
Giả sử không thoát hơi nước thì 200 gam nước sẽ hòa tan tối đa x mol KAl(SO4)2.12H2O được dung dịch bão hòa ở 20oC.
Phương trình nồng độ dung dịch bão hòa: \[C\% = \frac{{{m_{ct}}}}{{{m_{{\rm{dd}}}}}}.100\% \to x\]
→ mKAl(SO4)2.12H2O.
Giải chi tiết:
Gọi x là số mol KAl(SO4)2.12H2O kết tinh.
Vì nhiệt độ không đổi nên độ tan cũng không đổi do đó nồng độ dung dịch bão hòa không đổi.
Giả sử không thoát hơi nước thì 200 gam nước sẽ hòa tan tối đa x mol KAl(SO4)2.12H2O được dung dịch bão hòa ở 20oC.
Phương trình nồng độ dung dịch bão hòa: \[C\% = \frac{{{m_{ct}}}}{{{m_{{\rm{dd}}}}}}.100\% = \frac{{258x}}{{474x + 200}}.100\% = 5,56\% \]
→ x = 0,048.
→ mKAl(SO4)2.12H2O = 0,048.474 = 22,75 gam.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận