Cho hình nón có chiều cao \(h = 10\) và bán kính đáy \(r = 5\). Xét hình trụ có một đáy nằm trên hình tròn đáy của hình nón, đường tròn đáy còn lại nằm trên mặt xung quanh của hình nón sao cho thể tích khối trụ lớn nhất. Khi đó, bán kính đáy của hình trụ bằng:
Cho hình nón có chiều cao \(h = 10\) và bán kính đáy \(r = 5\). Xét hình trụ có một đáy nằm trên hình tròn đáy của hình nón, đường tròn đáy còn lại nằm trên mặt xung quanh của hình nón sao cho thể tích khối trụ lớn nhất. Khi đó, bán kính đáy của hình trụ bằng:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Phương pháp giải:
- Đặt bán kính khối trụ là \(r\). Sử dụng định lí Ta-lét tính chiều cao khối trụ theo \(r\).
- Tính thể tích khối trụ có chiều cao \(h\), bán kính đáy \(r\) là \(V = \pi {r^2}h\).
Giải chi tiết:
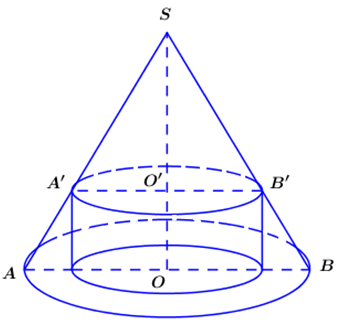
Theo bài ra ta có \(SO = 10,{\mkern 1mu} {\mkern 1mu} OA = 5\)
Đặt \(O'A' = r{\rm{ }}\left( {0 < r < 5} \right)\)
Áp dụng định lí Ta-lét ta có \(\frac{{O'A'}}{{OA}} = \frac{{SO'}}{{SO}} \Rightarrow \frac{r}{5} = \frac{{SO'}}{{10}} \Leftrightarrow SO' = 2r \Rightarrow OO' = 10 - 2r\)
Khi đó thể tích khối trụ là: \(V = \pi .O'{A'^2}.OO' = \pi .{r^2}\left( {10 - 2r} \right) = 2\pi \left( { - {r^3} + 5{r^2}} \right)\).
Xét hàm số \(f\left( r \right) = - {r^3} + 5{r^2}\) trên \(\left( {0;5} \right)\) ta có \(f'\left( r \right) = - 3{r^2} + 10r = 0 \Leftrightarrow \left[ \begin{array}{l}r = 0{\rm{ }}\left( {ktm} \right)\\r = \frac{{10}}{3}\end{array} \right.\).
Vậy để thể tích khối trụ đạt GTLN thì bán kính khối trụ bằng \(\frac{{10}}{3}\).
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(1,50{\mkern 1mu} {m^3}\)
Phương pháp giải:
- Gọi chiều rộng, chiều dài, chiều cao của bể lần lượt là \(x,2x,y\)
- Tìm mối liên hệ \(x,y\) dựa vào dữ kiện diện tích \(6,5{m^2}\).
- Lập hàm số thể tích theo ẩn \(x\) và xét hàm tìm \({V_{\max }}\).
Giải chi tiết:
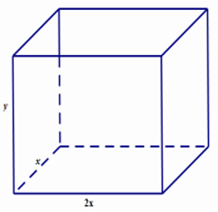
Gọi chiều rộng, chiều dài, chiều cao của bể lần lượt là \(x,2x,y{\mkern 1mu} {\mkern 1mu} \left( {x,y > 0} \right)\).
Diện tích phần lắp kính là: \(2x.x + 2xy + 2.2x.y = 2{x^2} + 6xy = 6,5\)
\( \Leftrightarrow xy = \frac{{6,5 - 2{x^2}}}{6} > 0 \Rightarrow x < \sqrt {\frac{{6,5}}{2}} = \frac{{\sqrt {13} }}{2}.\)
Thể tích bể cá là: \(V = 2x.x.y = 2x.\frac{{6,5 - 2{x^2}}}{6} = \frac{{ - 4{x^3} + 13x}}{6}\) với \(0 < x < \frac{{\sqrt {13} }}{2}\)
Ta có: \(V' = \frac{{ - 12{x^2} + 13}}{6},V' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{{\sqrt {39} }}{6}}\\{x = - \frac{{\sqrt {39} }}{6}\left( L \right)}\end{array}} \right.\)
Bảng biến thiên:
Vậy \({V_{\max }} = \frac{{13\sqrt {39} }}{{54}} \approx 1,50{\mkern 1mu} {m^3}\).
Lời giải
Đáp án A
Phương pháp giải:
Căn cứ 6 phương thức biểu đạt đã học (miêu tả, tự sự, biểu cảm, nghị luận, thuyết minh, hành chính – công vụ).
Giải chi tiết:
Phương thức biểu đạt tự sự.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo