Cho khối lăng trụ tam giác đều \[ABC.A'B'C'\] có cạnh đáy là \[2a\] và khoảng cách từ điểm \[A\] đến mặt phẳng \[\left( {A'BC} \right)\] bằng \[a\]. Tính thể tích của khối lăng trụ \[ABC.A'B'C'\]
Cho khối lăng trụ tam giác đều \[ABC.A'B'C'\] có cạnh đáy là \[2a\] và khoảng cách từ điểm \[A\] đến mặt phẳng \[\left( {A'BC} \right)\] bằng \[a\]. Tính thể tích của khối lăng trụ \[ABC.A'B'C'\]
D. \[\frac{{3{a^3}\sqrt 2 }}{2}\]
Quảng cáo
Trả lời:
Đáp án D
Phương pháp giải:
- Xác định góc từ điểm \[A\] đến \(\left( {A'BC} \right)\)
- Sử dụng hệ thức lượng trong tam giác vuông tính \(A'A\)
- Tính thể tích \({V_{ABC.A'B'C'}} = A'A.{S_{\Delta ABC}}\)
Giải chi tiết:
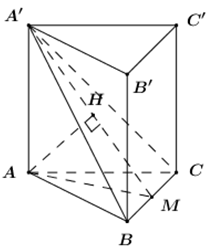
Gọi \(M\) là trung điểm của \[BC\] ta có \[\left\{ {\begin{array}{*{20}{l}}{BC \bot AM}\\{BC \bot AA'}\end{array}} \right. \Rightarrow BC \bot \left( {A'BC} \right)\]
Trong \[\left( {A'BC} \right)\] kẻ \[AH \bot A'M{\mkern 1mu} {\mkern 1mu} \left( {H \in A'M} \right)\] ta có: \[\left\{ {\begin{array}{*{20}{l}}{AH \bot BC}\\{AH \bot A'M}\end{array}} \right. \Rightarrow AH \bot \left( {A'BC} \right)\]
\[ \Rightarrow d\left( {A;\left( {A'BC} \right)} \right) = AH = a\]
Vì tam giác \(ABC\) đều cạnh \(2a\) nên \(AM = 2a.\frac{{\sqrt 3 }}{2} = a\sqrt 3 \) và \({S_{\Delta ABC}} = {\left( {2a} \right)^2}\frac{{\sqrt 3 }}{4} = {a^2}\sqrt 3 \)
Áp dụng hệ thức lượng trong tam giác vuông \(AA'M\) ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A'{A^2}}} + \frac{1}{{A{M^2}}} \Rightarrow \frac{1}{{{a^2}}} = \frac{1}{{A'{A^2}}} + \frac{1}{{3{a^2}}}\)
\( \Rightarrow \frac{1}{{A'{A^2}}} = \frac{2}{{3{a^2}}} \Rightarrow A'A = \frac{{a\sqrt 6 }}{2}\)
Vậy \({V_{ABC.A'B'C'}} = A'A.{S_{\Delta ABC}} = \frac{{a\sqrt 6 }}{2}.{a^2}\sqrt 3 = \frac{{3{a^3}\sqrt 2 }}{2}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(1,50{\mkern 1mu} {m^3}\)
Phương pháp giải:
- Gọi chiều rộng, chiều dài, chiều cao của bể lần lượt là \(x,2x,y\)
- Tìm mối liên hệ \(x,y\) dựa vào dữ kiện diện tích \(6,5{m^2}\).
- Lập hàm số thể tích theo ẩn \(x\) và xét hàm tìm \({V_{\max }}\).
Giải chi tiết:
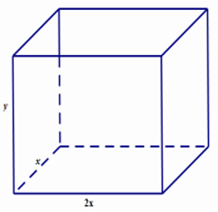
Gọi chiều rộng, chiều dài, chiều cao của bể lần lượt là \(x,2x,y{\mkern 1mu} {\mkern 1mu} \left( {x,y > 0} \right)\).
Diện tích phần lắp kính là: \(2x.x + 2xy + 2.2x.y = 2{x^2} + 6xy = 6,5\)
\( \Leftrightarrow xy = \frac{{6,5 - 2{x^2}}}{6} > 0 \Rightarrow x < \sqrt {\frac{{6,5}}{2}} = \frac{{\sqrt {13} }}{2}.\)
Thể tích bể cá là: \(V = 2x.x.y = 2x.\frac{{6,5 - 2{x^2}}}{6} = \frac{{ - 4{x^3} + 13x}}{6}\) với \(0 < x < \frac{{\sqrt {13} }}{2}\)
Ta có: \(V' = \frac{{ - 12{x^2} + 13}}{6},V' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{{\sqrt {39} }}{6}}\\{x = - \frac{{\sqrt {39} }}{6}\left( L \right)}\end{array}} \right.\)
Bảng biến thiên:

Vậy \({V_{\max }} = \frac{{13\sqrt {39} }}{{54}} \approx 1,50{\mkern 1mu} {m^3}\).
Câu 2
B. Phương thức biểu đạt nghị luận
Lời giải
Đáp án A
Phương pháp giải:
Căn cứ 6 phương thức biểu đạt đã học (miêu tả, tự sự, biểu cảm, nghị luận, thuyết minh, hành chính – công vụ).
Giải chi tiết:
Phương thức biểu đạt tự sự.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
D. \(\frac{8}{3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
B. khai thác gỗ tròn, trồng cây dược liệu
D. khai thác các khoáng sản, sản xuất ô tô
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
B. Tơ tằm thuộc loại tơ thiên nhiên.
D. Tơ visco thuộc loại tơ tổng hợp.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
