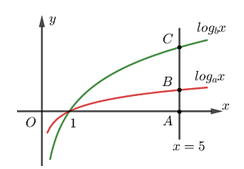
Từ một tấm tôn dạng hình tam giác vuông với hai cạnh góc vuông bằng \[3m\] và \[4m,\] một anh thợ cần cắt một tấm tôn có dạng hình chữ nhật nội tiếp tam giác trên. Anh ta gò tấm tôn hình chữ nhật này thành một hình trụ không đáy (như hình vẽ) để đổ thóc vào trong. Thể tích lớn nhất của khối trụ thu được gần nhất với kết quả nào dưới đây?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án A
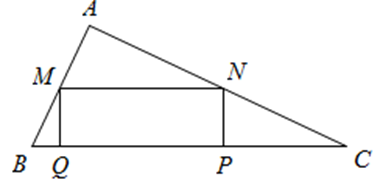
Khối trụ thu được có thể tích là \[V = \pi {R^2}h\].
\[\begin{array}{l}\Delta BQM\~\Delta BAC \Rightarrow \frac{{QM}}{{AC}} = \frac{{BQ}}{{BA}} \Rightarrow \frac{h}{4} = \frac{{BQ}}{3} \Rightarrow BQ = \frac{{3h}}{4}.\\\Delta CPN\~\Delta CAB \Rightarrow \frac{{PN}}{{AB}} = \frac{{CP}}{{CA}} \Rightarrow \frac{h}{4} = \frac{{CP}}{3} \Rightarrow CP = \frac{{4h}}{3}.\end{array}\]
Do đó \[PQ = BC - BQ - CP = 5 - \frac{{3h}}{4} - \frac{{4h}}{3} = 5 - \frac{{25h}}{{12}} = \frac{{60 - 25h}}{{12}}\].
Mà \[2R\pi = PQ \Rightarrow R = \frac{{60 - 25h}}{{24\pi }} \Rightarrow V = \pi {\left( {\frac{{60 - 25h}}{{24\pi }}} \right)^2}h = \frac{{h{{\left( {25h - 60} \right)}^2}}}{{{{24}^2}\pi }} = f\left( h \right)\].
\[f'\left( h \right) = \frac{{{{\left( {25h - 60} \right)}^2} + h.2\left( {25h - 60} \right).25}}{{{{24}^2}\pi }} = 0 \Rightarrow h = \frac{4}{5} \Rightarrow V \le f\left( {\frac{4}{5}} \right) \approx 0,71\;{m^3}.\]
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án C
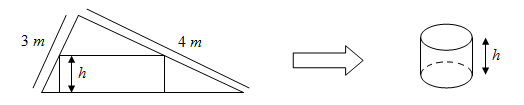
Ta có \[\begin{array}{l}C\left( {5;{{\log }_b}5} \right),B\left( {5;{{\log }_a}5} \right),A\left( {5;0} \right);\overrightarrow {CB} = 2\overrightarrow {BA} \Rightarrow {\log _a}5 - {\log _b}5 = 2\left( { - {{\log }_a}5} \right)\\ \Rightarrow 3{\log _a}5 = {\log _b}5 \Rightarrow \frac{3}{{{{\log }_5}a}} = \frac{1}{{{{\log }_5}b}} \Rightarrow {\log _5}a = 3{\log _5}b = {\log _5}{b^3} \Rightarrow a = {b^3}.\end{array}\]
Lời giải
Đáp án D
Gọi \[M = d \cap d'\], ta có \[d':\left\{ \begin{array}{l}x = 2 + t\\y = - 1 - t\\z = 1 + t\end{array} \right.\;\left( {t \in \mathbb{R}} \right) \Rightarrow M\left( {t + 2; - t - 1;t + 1} \right)\].
Đường thẳng d qua \[A\left( {1; - 1;3} \right)\] và nhận \[\overrightarrow {AM} = \left( {t + 1; - t;t - 2} \right)\] là một VTCP.
Mặt phẳng \[\left( P \right):x + 4y - 2z + 1 = 0\] nhận \[\overrightarrow n = \left( {1;4; - 2} \right)\] là một VTPT.
Ta có \[d//\left( P \right) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AM} .\overrightarrow n = 0\\A \notin \left( P \right)\end{array} \right. \Leftrightarrow \left( {t + 1} \right) - 4t - 2\left( {t - 2} \right) = 0 \Leftrightarrow t = 1 \Rightarrow \overrightarrow {AM} = \left( {2; - 1; - 1} \right)\].
Đường thẳng d qua \[A\left( {1; - 1;3} \right)\] và nhận \[\overrightarrow {AM} = \left( {2; - 1; - 1} \right)\] là một VTCP
\[ \Rightarrow d:\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 3}}{{ - 1}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo