Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D
Vì tanα = ‒3 nên do đó cosα ≠ 0
Ta có:
(do cosα ≠ 0)
Vậy
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Ta có:
cos180° = cos(180° ‒ 0°) = ‒cos0° Þ cos0° + cos180° = 0;
cos179° = cos(180° ‒ 1°) = ‒cos1° Þ cos1° + cos179° = 0;
cos178° = cos(180° ‒ 2°) = ‒cos2° Þ cos2° + cos178° = 0;
…
cos91° = cos(180° ‒ 89°) = ‒cos89° Þ cos89° + cos91° = 0.
Suy ra: P = cos0° + cos1° + cos2° + ... + cos178° + cos179° + cos180°
= (cos0° + cos180°) + (cos1° + cos179°) + ... + (cos89° + cos91°) + cos90°
= 0 + 0 + ... + 0 + 0
= 0.
Do đó P = 0.
Vậy giá trị của biểu thức P = 0 thuộc khoảng (‒1;1).
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho ![]() . Gọi (x0; y0) là toạ độ điểm M, ta có:
. Gọi (x0; y0) là toạ độ điểm M, ta có:
- Tung độ y0 của M là sin của góc α, kí hiệu là sinα = y0;
- Hoành độ x0 của M là côsin của góc α, kí hiệu là cosα = x0;
- Tỉ số (x0 ≠ 0) là tang của góc α, kí hiệu là
- Tỉ số (y0 ≠ 0) là côtang của góc α, kí hiệu là
Gọi H và K lần lượt là hình chiếu của M lên Ox và Oy.
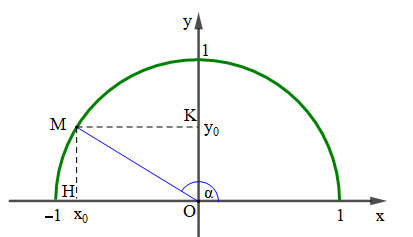
Khi đó ta có: OH = x0 = cosα, MH = OK = y0 = sinα, OM = 1.
Tam giác OMH vuông tại H, áp dụng định lí Pythagore ta có:
MH2 + OH2 = OM2
Hay sin2α + cos2α = 1.
Do đó phương án A là mệnh đề đúng.
Với 0° < α < 180° và α ≠ 90° ta có:
Do đó phương án B là mệnh đề đúng.
Với α ≠ 90° ta có: (do sin2α + cos2α = 1).
Do đó phương án C là mệnh đề đúng.
Với 0° < α < 180° và α ≠ 90° ta có:
(do sin2α + cos2α = 1).
Do đó phương án D là mệnh đề sai.
Vậy ta chọn phương án D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.