Câu hỏi:
24/07/2022 404Cho hình chóp S.ABCD có đáy là hình chữ nhật, cạnh \[AB = 2a.\] Tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng \[\left( {ABCD} \right).\] Khoảng cách từ điểm D đến mặt phẳng (SBC) bằng
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án C
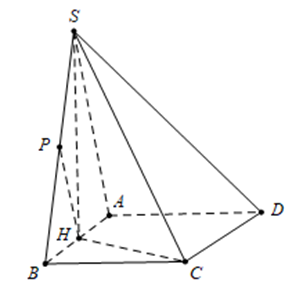
Kẻ \(SH \bot AB \Rightarrow SH \bot \left( {ABCD} \right).\)
Ta có \(AD//BC \Rightarrow AD//\left( {SBC} \right)\)
\( \Rightarrow d\left( {D;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right) = 2d\left( {H;\left( {SBC} \right)} \right).\)
Kẻ \(HP \bot SB \Rightarrow d\left( {H;\left( {SBC} \right)} \right) = HP\)
\( \Rightarrow d\left( {D;\left( {SBC} \right)} \right) = 2HP = d.\)
Ta có \(\frac{1}{{H{P^2}}} = \frac{1}{{H{B^2}}} + \frac{1}{{H{S^2}}}.\)
Cạnh \(HB = \frac{{AB}}{2} = a;SH = \frac{{AB}}{2} = a\)
\( \Rightarrow HP = \frac{a}{{\sqrt 2 }} \Rightarrow d = a\sqrt 2 .\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án D
Ta có \({u_6} = {u_1}{q^5} \Rightarrow \frac{3}{{32}} = 3{q^5} \Rightarrow q = \frac{1}{2}.\)
Lời giải
Đáp án D
Ta có \(\int {\frac{1}{{4x + 1}}dx} = \frac{1}{4}\ln \left| {4x + 1} \right| + C.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải