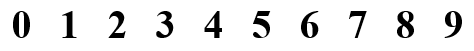Bộ 5 đề thi cuối kì 1 Toán 6 Cánh diều cấu trúc mới có đáp án - Đề 4
8 người thi tuần này 4.6 35 lượt thi 5 câu hỏi 60 phút
🔥 Đề thi HOT:
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
10 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Bài 1: Tập hợp. Phần tử của tập hợp (có đáp án)
5 câu Trắc nghiệm Toán 6 Cánh diều Bài 1: Tập hợp có đáp án ( Nhận biết )
11 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Bài 1: Các dạng toán về tập hợp, phần tử của tập hợp ( có đáp án )
20 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án (Phần 2)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
1. a) Các số vừa có trục đối xứng, vừa có tâm đối xứng là số 0, 8.
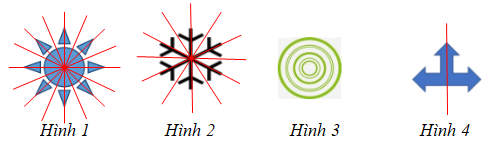
b) Hình 1 có 8 trục đối xứng;
Hình 2 có 6 trục đối xứng;
Hình 3 có vô số trục đối xứng là các đường kính của hình tròn.
Hình 4 có 1 trục đối xứng.
2. a) Diện tích một mặt của hộp giấy là: \(\frac{{\left( {10 + 13} \right).20}}{2} = 230\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\)
Vậy diện tích một mặt bên của hộp giấy là \(230\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}.\)
b) Diện tích bốn mặt xung quanh của chiếc hộp là: \(230.\,4\,\, = \,\,920\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\)
Đáy hộp đựng bỏng ngô là hình vuông nên có diện tích là: \(10.\,10 = \,100\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\)
Diện tích giấy bìa ít nhất để làm được một chiếc hộp là: \(920\, + \,100\,\, = \,1020\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).
Vậy cần ít nhất \(1020\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\) giấy bìa để làm một chiếc hộp đựng bỏng ngô đó.
Lời giải
Hướng dẫn giải
Tổng khối lượng xoài và xam lúc đầu là:
\(65 + 71 + 58 + 72 + 93 = 359\) (kg).
Vì sau khi bán một giỏ cam khối lượng xoài gấp ba lần số lượng cam còn lại nên tổng khối lượng xoài và cam còn lại là một số chia hết cho 4.
Mà số \(359\) chia 4 dư 3 nên giỏ cam bán đi phải có khối lượng là một số chia 4 dư 3.
Trong các số \(65,\,\,71,\,\,58,\,\,72,\,\,93\) thì chỉ có số \(71\) chia 4 dư 3.
Như vậy, giỏ cam bán đi là giỏ có khối lượng \[71{\rm{\;kg}}{\rm{.}}\]
Khối lượng xoài và cam còn lại là: \(359 - 71 = 288{\rm{\;(kg)}}{\rm{.}}\)
Khối lượng cam còn lại là: \(288:4 = 72{\rm{\;(kg)}}{\rm{.}}\)
Vậy, các giỏ cam là các giỏ có khối lượng: \[71{\rm{\;kg}},\,\,72{\rm{\;kg;}}\] các giỏ xoài là các giỏ có khối lượng \[65{\rm{\;kg,}}\,\,58{\rm{\;kg}},\,\,93{\rm{\;kg}}.\]
Lời giải
Hướng dẫn giải
|
a) \({2^3} \cdot {2^2} + {4^4}:{4^4} - {2^0}\) \( = {2^5} + 1 - 1\) \( = 32\). c) \(27 \cdot 121 - 87 \cdot 27 + 73 \cdot 34\) \( = 27 \cdot \left( {121 - 87} \right) + 73 \cdot 34\) \( = 27 \cdot 34 + 73 \cdot 34\) \( = 34 \cdot \left( {27 + 73} \right)\) \( = 34 \cdot 100\) \( = 3\,\,400\). |
b) \(\left( { - 4} \right) \cdot 8 \cdot \left( { - 125} \right) \cdot \left( { - 3} \right)\) \( = \left[ {8 \cdot \left( { - 125} \right)} \right] \cdot \left[ {\left( { - 4} \right) \cdot \left( { - 3} \right)} \right]\) \[ = \left( { - 1\,\,000} \right) \cdot 12\] \( = - 12\,\,000\). d) \(2\,\,353 - \left( {473 + 2\,\,153} \right) + \left( { - 55 + 373} \right)\) \( = 2\,\,353 - 473 - 2\,\,153 - 55 + 373\) \( = \left( {2\,\,353 - 2\,\,153} \right) + \left( { - 473 + 373} \right) - 55\) \( = 200 + \left( { - 100} \right) - 55\) \( = 100 - 55\) \( = 45\). |
Lời giải
Hướng dẫn giải
|
a) \(9 \cdot \left( {x + 2} \right) - 28 = 26\) \(9 \cdot \left( {x + 2} \right) = 54\) \(x + 2 = 6\) \(x = 4\) Vậy \(x = 4.\) |
b) \(\left( { - 6 + 3x} \right):5 = - 18\) \( - 6 + 3x = - 90\) \(3x = - 84\) \(x = - 28\). Vậy \(x = - 28\). |
c) \({\left( {4 - x} \right)^3} + 17 = - 10\) \({\left( {4 - x} \right)^3} = - 27\) \({\left( {4 - x} \right)^3} = {\left( { - 3} \right)^3}\) Suy ra \(4 - x = - 3\) \(x = 4 - \left( { - 3} \right)\) \(x = 7\) Vậy \(x = 7.\) |
Lời giải
Hướng dẫn giải
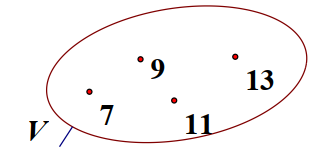
1. Mô tả tập hợp \(V\) bằng cách nêu dấu hiệu đặc trưng cho các phần tử của tập hợp:
\(V = \{ x|x\) là số tự nhiên lẻ, \(7 \le x \le 13\} \).
2. Số điểm của anh An là: \(5 \cdot 500 + 3 \cdot \left( { - 200} \right) = 1\,\,900\) (điểm)
Số điểm của chị Lan là: \(3 \cdot 500 + 5 \cdot \left( { - 200} \right) = 500\) (điểm)
Số điểm của chị Trang là: \(6 \cdot 500 + 2 \cdot \left( { - 200} \right) = 2\,\,600\) (điểm)
Vì \(2\,\,600 > 1\,\,900 > 500\) nên điểm của chị Trang cao điểm nhất.
Vậy trong 3 người thì chị Trang là người cao điểm nhất.
3. Số học sinh trong mỗi nhóm càng nhỏ thì số nhóm cần chia càng lớn.
Gọi số nhóm lớn nhất cần chia sao cho số học sinh trong mỗi nhóm ít nhất là \(x\) \(\left( {x \in \mathbb{N}} \right)\).
Để chia 60 học sinh nam và 48 học sinh nữ vào các nhóm sao cho số học sinh nam trong mỗi nhóm bằng nhau và số học sinh nữ trong mỗi nhóm bằng nhau thì \(60\,\, \vdots \,\,x,\,\,48\,\, \vdots \,\,x\)
Mà số nhóm cần chia là lớn nhất nên \(x = \)ƯCLN\(\left( {60,48} \right)\).
Ta có: \(60 = {2^2}.3.5;\,\,\,\,\,\,\,\,48 = {2^4}.3\).
Suy ra \(x = \)ƯCLN\(\left( {60,48} \right) = {2^2}.3 = 12\).
Vậy số nhóm cần chia là \(12\) nhóm.
Khi đó số học sinh nam trong mỗi nhóm là: \(60:12 = 5\) (học sinh);
Số học sinh nữ trong mỗi nhóm là: \(48:12 = 4\) (học sinh).