Bài tập cuối chương 1

a) 4 . 25 – 12 . 5 + 170 : 10 

= 100 – 60 + 17               

= 40 + 17 

= 57.

b) (7 + 3³ : 3²) . 4 – 3

= (7 + 3^{3 – 2}) . 4 – 3 

= (7 + 3¹) . 4 – 3 

= (7 + 3) . 4 – 3

= 10 . 4 – 3

= 40 – 3 = 37.

c) 12 : {400 : [500 – (125 + 25 . 7)]}

= 12 : {400 : [500 – (125 + 175)]}

= 12 : [400 : (500 – 300)]

= 12 : (400 : 200) 

= 12 : 2 

= 6.

d) 168 + {[2 . (2⁴ + 3²) – 256⁰] : 7²}

= 168 + {[2 . (16 + 9) – 1] : 49}

= 168 + [(2. 25 – 1) : 49]

= 168 + [(50 – 1) : 49]

= 168 + (49 : 49)

= 168 + 1 = 169. 

Ta có: P là tập hợp các số nguyên tố.

a) Vì 2 chỉ có hai ước là 1 và chính nó nên 2 là số nguyên tố hay 2 thuộc P.

Do đó 2  P. 

b) Vì 47 chỉ có hai ước là 1 và 47, nên 47 là số nguyên tố hay 47 thuộc P. 

Do đó 47  P. 

c) Ta có: a = 3 . 5 . 7 . 9 + 20 = 15 . 7 . 9 + 20 = 105 . 9 + 20 = 945 + 20 = 965

Vì 965 : 5 = 193 nên số 965 ngoài có hai ước là 1 và 965, còn có thêm ít nhất một ước nữa là 5 nên 965 hay a là hợp số.

Do đó a không phải là số nguyên tố nên a không thuộc P.

Vậy a 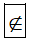 P. 

d) Ta có: b = 5 . 7 . 11 + 13 . 17 = 35 . 11 + 221 = 385 + 221 = 606

Vì 606 : 6 = 101 nên số 606 ngoài có hai ước là 1 và 606, còn có thêm ít nhất một ước nữa là 6 nên 606 là hợp số hay b là hợp số.

Do đó b không phải là số nguyên tố nên b không thuộc P.

Vậy b 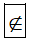 P. 

Ta có thể phân tích một số ra thừa số nguyên tố bằng cách viết "theo cột dọc" hoặc "rẽ nhánh".

a) Ta có:

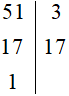
Vậy 51 = 3 . 17.

b) Ta có: 

Vậy 76 = 2 . 2 . 19 = 2² . 19.

c) Ta có: 

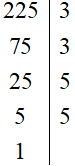
Vậy 225 = 3 . 3 . 5 . 5 = 3² . 5². 

 d) Ta có: 1 800 = 10 . 180 

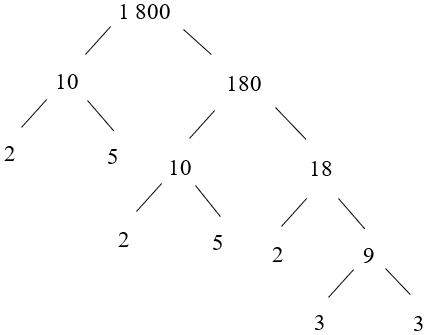
Vậy 1 800 = 2 . 5 . 2 . 5 . 2 . 3 . 3 = 2³ . 3² . 5².

a) 40 và 60

Ta có: 

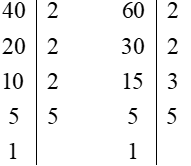
Do đó: 40 = 2 . 2 . 2 . 5 = 2³ . 5 

60 = 2 . 2 . 3 . 5 = 2² . 3 . 5

Các thừa số nguyên tố chung của 40 và 60 là 2 và 5

Số 2 có số mũ nhỏ nhất là 2; số 5 có số mũ nhỏ nhất là 1

Vậy ƯCLN(40, 60) = 2² . 5¹ = 4 . 5 = 20.

b) 16 và 124

Ta có: 16 = 2⁴ 

Lại có 

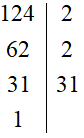
Do đó: 124 = 2 . 2 . 31 = 2² . 31

Thừa số nguyên tố chung của 16 và 124 là 2, với số mũ nhỏ nhất là 2.

Vậy ƯCLN(16, 124) = 2² = 4. 

c) 41 và 47

Ta có: số 41 chỉ có hai ước là 1 và 41 nên 41 là số nguyên tố

Số 47 chỉ có hai ước là 1 và 47 nên 47 cũng là số nguyên tố

Do đó 41 và 47 là hai số nguyên tố cùng nhau.

Vậy ƯCLN(41, 47) = 1.

a) 72 và 540 

Ta có: 

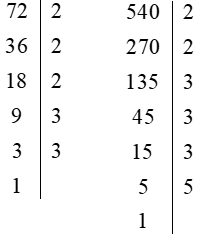
Do đó: 72 = 2 . 2 . 2 . 3 . 3 = 2³ . 3²

540 = 2 . 2 . 3 . 3 . 3 . 5 = 2² . 3³ . 5

Các thừa số nguyên tố chung và riêng của 72 và 540 là 2, 3, 5

Số hai có số mũ lớn nhất là 3; số 3 có số mũ lớn nhất là 3; số 5 có số mũ lớn nhất là 1.

Vậy BCNN(72, 540) = 2³ . 3³ . 5¹ = 8 . 27 . 5 = 1 080.

b) 28, 49, 64 

Ta có: 28 = 4 . 7 = 2² . 7

49 = 7²; 64 = 2⁶ 

Các thừa số nguyên tố chung và riêng của 28, 49 và 64 là 2, 7

Số 2 có số mũ lớn nhất là 6, số 7 có số mũ lớn nhất là 2.

Vậy BCNN(28, 49, 64) = 2⁶ . 7² = 64 . 49 = 3 136.

c) 43 và 53

Ta có: 43 chỉ có hai ước là 1 và 43 nên 43 là số nguyên tố

53 chỉ có hai ước là 1 và 53 nên nó cũng là số nguyên tố

Do đó 43 và 53 là hai số nguyên tố cùng nhau.

Vậy BCNN(43, 53) = 43 . 53 = 2 279.