Câu hỏi:
13/07/2024 3,332
Tính các góc chưa biết của tam giác ABC trong các trường hợp sau:
AB = 15, AC = 25, BC = 30.
Tính các góc chưa biết của tam giác ABC trong các trường hợp sau:
AB = 15, AC = 25, BC = 30.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Theo định lí côsin ta có: AB2 = BC2 + AC2 – 2BC.AC.cos\(\widehat {\rm{C}}\)
⇒ cos\(\widehat {\rm{C}}\) = \(\frac{{{\rm{B}}{{\rm{C}}^2} + {\rm{A}}{{\rm{C}}^2} - {\rm{A}}{{\rm{B}}^2}}}{{2.{\rm{BC}}.{\rm{AC}}}}\) = \(\frac{{{{30}^2} + {{25}^2} - {{15}^2}}}{{2.30.25}}\) = \(\frac{{13}}{{15}}\) ⇒ \(\widehat {\rm{C}}\) ≈ 29°55’.
Tương tự như trên, ta có:
cos\(\widehat {\rm{A}}\) = \(\frac{{{\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} - {\rm{BC}}{^2}}}{{2.{\rm{AB}}.{\rm{AC}}}}\)= \(\frac{{{{15}^2} + {{25}^2} - {{30}^2}}}{{2.15.25}}\) = \(\frac{{ - 1}}{{15}}\) ⇒ \(\widehat {\rm{A}}\) ≈ 93°49’.
cos\(\widehat {\rm{B}}\) = \(\frac{{{\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^2} - {\rm{AC}}{^2}}}{{2.{\rm{AB}}.{\rm{BC}}}}\)= \(\frac{{{{15}^2} + {{30}^2} - {{25}^2}}}{{2.15.30}}\) = \(\frac{5}{9}\) ⇒ \(\widehat {\rm{B}}\) ≈ 56°15’.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
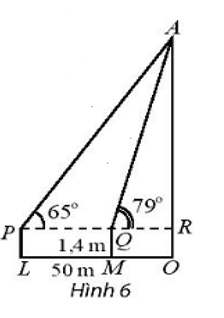
Đặt d = PQ = 50m; h = AR là chiều cao từ giác kế đến đỉnh tòa nhà.
Ta có: \(\widehat {{\rm{RQA}}}\)= 79° và \(\widehat {{\rm{RPA}}}\)= 65°
tan\(\widehat {{\rm{RQA}}}\) = \(\frac{{{\rm{AR}}}}{{{\rm{QR}}}}\) = \(\frac{{\rm{h}}}{{{\rm{QR}}}}\) ⇒ QR = \(\frac{{\rm{h}}}{{{\rm{tan}}\widehat {{\rm{RQA}}}}}\) = \(\frac{{\rm{h}}}{{{\rm{tan79^\circ }}}}\).
tan\(\widehat {{\rm{RPA}}}\) = \(\frac{{{\rm{AR}}}}{{{\rm{PR}}}}\) = \(\frac{{\rm{h}}}{{{\rm{PR}}}}\) ⇒ PR = \(\frac{{\rm{h}}}{{{\rm{tan}}\widehat {{\rm{RPA}}}}}\) = \(\frac{{\rm{h}}}{{{\rm{tan65^\circ }}}}\).
Ta có:
PQ = PR – QR = \(\frac{{\rm{h}}}{{{\rm{tan65^\circ }}}}\) – \(\frac{{\rm{h}}}{{{\rm{tan79^\circ }}}}\) = h \(\left( {\frac{1}{{\tan 65^\circ }} - \frac{1}{{\tan 79^\circ }}} \right)\) = 50 (m)
⇒ h ≈ 183,9 (m)
Vậy chiều cao của tòa nhà là AR + RO ≈ 183,9 + 1,4 = 185,3 (m).
Lời giải
Lời giải
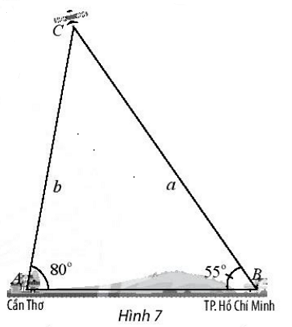
Tam giác ABC có: \(\widehat {\rm{A}}\) + \(\widehat {\rm{B}}\) + \(\widehat {\rm{C}}\) = 180°.
⇒ \(\widehat {\rm{C}}\) = 180° – \(\widehat {\rm{A}}\)– \(\widehat {\rm{B}}\) = 180° – 80° – 55° = 45°.
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{{\rm{AB}}}}{{{\rm{sinC}}}} = \frac{{{\rm{AC}}}}{{{\rm{sinB}}}}\) ⇒ AC = \(\frac{{{\rm{AB}}}}{{{\rm{sinC}}}}\).sinB = \(\frac{{127}}{{\sin 45^\circ }}\).sin55° ≈ 147 (km).
Vậy khoảng cách giữa trạm Cần Thơ và vệ tinh khoảng 147 km.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
50 câu trắc nghiệm Thống kê cơ bản (phần 1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận