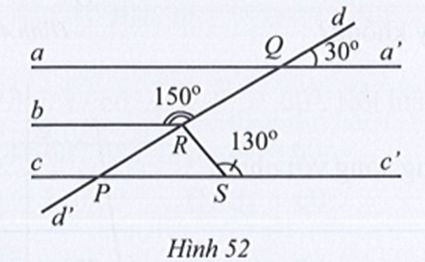
Quan sát Hình 51, biết Ox // HK, tia Ox là tia phân giác của góc yOK. Chứng minh hai góc OHK và OKH bằng nhau.
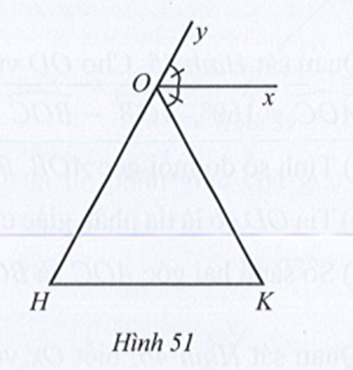
Quan sát Hình 51, biết Ox // HK, tia Ox là tia phân giác của góc yOK. Chứng minh hai góc OHK và OKH bằng nhau.

Câu hỏi trong đề: Giải SBT Toán 7 Bài tập cuối chương 4 có đáp án !!
Quảng cáo
Trả lời:
Vì Ox là tia phân giác của góc yOK nên
Do Ox // HK nên ta có:
• (hai góc đồng vị);
• (hai góc so le trong).
Do đó (cùng bằng và ).
Vậy
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
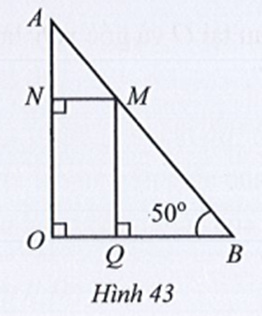
Ta có (hai góc kề bù)
Suy ra
Do đó (cùng bằng 90°)
Mà và ở vị trí đồng vị nên MN // OB.
Suy ra:
• (hai góc so le trong)
• (hai góc đồng vị).
Ta có (hai góc kề nhau).
Mà (hai góc kề bù).
Do đó
Suy ra
Ta lại có: (cùng bằng 90°)
Mà và ở vị trí đồng vị nên MQ // AO.
Suy ra (hai góc đồng vị).
Vậy và
Lời giải
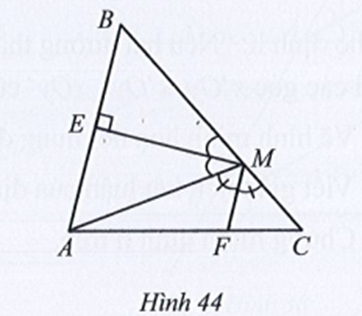
Vì ME, MF lần lượt là tia phân giác của góc AMB và AMC nên:
và
Mặt khác và là hai góc kề bù nên ta có:
Lại có và là hai góc kề nhau nên:
Do đó \
Hay
Suy ra (cùng bằng 90°).
Mà là hai góc so le trong nên MF // AB.
Vậy MF và AB song song với nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.