Giải SBT Toán 7 Bài tập cuối chương 4 có đáp án

31 người thi tuần này 4.6 1.6 K lượt thi 23 câu hỏi

Đề số 1

🔥 Đề thi HOT:

4408 người thi tuần này

Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1

20.4 K lượt thi 17 câu hỏi

848 người thi tuần này

Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2

16.8 K lượt thi 17 câu hỏi

704 người thi tuần này

Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04

6.1 K lượt thi 30 câu hỏi

608 người thi tuần này

15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án

14.1 K lượt thi 15 câu hỏi

565 người thi tuần này

Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01

5.6 K lượt thi 23 câu hỏi

408 người thi tuần này

Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01

5.8 K lượt thi 21 câu hỏi

272 người thi tuần này

Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 3

16.2 K lượt thi 29 câu hỏi

272 người thi tuần này

Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 02

5.3 K lượt thi 23 câu hỏi

Nội dung liên quan:

Bài tập Góc ở vị trí đặc biệt có đáp án

1100 lượt thi

1 đề

Giải SBT Toán 7 Bài 1. Góc ở vị trí đặc biệt có đáp án

1514 lượt thi

1 đề

Giải VBT Toán 7 Cánh diều Bài 1. Góc ở vị trí đặc biệt có đáp án

1285 lượt thi

1 đề

Bài tập Tia phân giác của một góc có đáp án

971 lượt thi

1 đề

Giải SBT Toán 7 Bài 2. Tia phân giác của một góc có đáp án

1525 lượt thi

1 đề

Giải VBT Toán 7 Cánh diều Bài 2. Tia phân giác của một góc có đáp án

1342 lượt thi

1 đề

Bài tập Hai đường thẳng song song có đáp án

1482 lượt thi

1 đề

Giải SBT Toán 7 Bài 3. Hai đường thẳng song song có đáp án

1274 lượt thi

1 đề

Giải VBT Toán 7 Cánh diều Bài 3. Hai đường thẳng song song có đáp án

1298 lượt thi

1 đề

Bài tập Định lí có đáp án

1147 lượt thi

1 đề

Danh sách câu hỏi:

Câu 1

Số đo của góc xOt trong Hình 39 là:

A. 45°;

B. 135°;

C. 55°;

D. 90°.

Lời giải

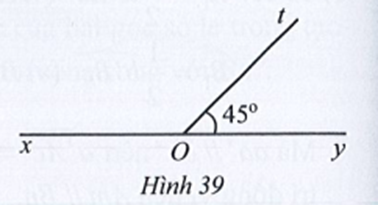
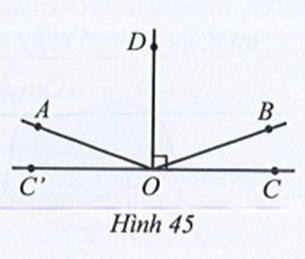
Ta có $\hat{x O t} + \hat{t O y} = 180 °$ (hai góc kề bù)

Nên $\hat{x O t} = 180 ° - \hat{t O y}$

Suy ra $\hat{x O t} = 180 ° - 45 ° = 135 ° .$

Vậy ta chọn phương án B.

Câu 2

Ở Hình 40 có AB và CD cắt nhau tại O, Ot là tia phân giác của góc BOC, $\hat{A O C} - \hat{B O C} = 68 ° .$ Số đo góc BOt là:

A. 56°;

B. 62°;

C. 28°;

D. 23°.

Lời giải

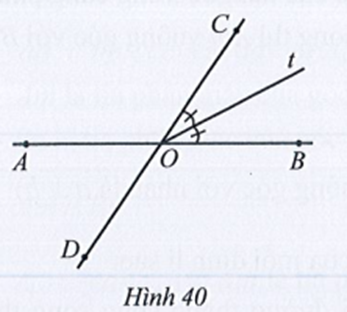
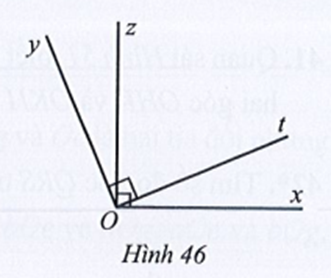
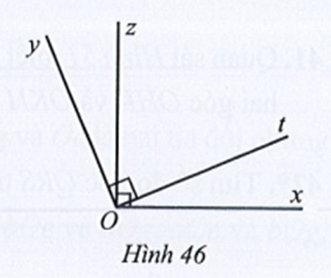
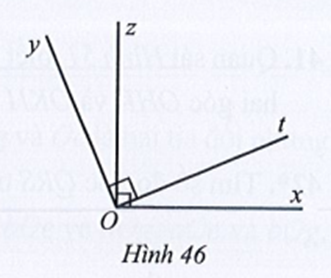
Ta có $\hat{A O C} + \hat{B O C} = 180 °$ (hai góc kề bù)

Mà $\hat{A O C} - \hat{B O C} = 68 °$

Suy ra $\hat{A O C} = \frac{180 ° + 68 °}{2} = 124 °$ và $\hat{B O C} = \frac{180 ° - 68 °}{2} = 56 ° .$

Vì Ot là tia phân giác của góc BOC nên ta có: $\hat{B O t} = \hat{t O C} = \frac{1}{2} \hat{B O C} = \frac{1}{2} .56 ° = 28 ° .$

Vậy ta chọn phương án C.

Câu 3

Cho Hình 41 có ${\hat{A}}_{1} = {\hat{B}}_{3} = 60 ° .$ Kết luận nào sau đây là sai?

A. ${\hat{A}}_{3} = 60 °;$

B. ${\hat{B}}_{1} = 60 °;$

C. ${\hat{A}}_{4} = 120 °;$

D. ${\hat{B}}_{2} = 60 ° .$

Lời giải

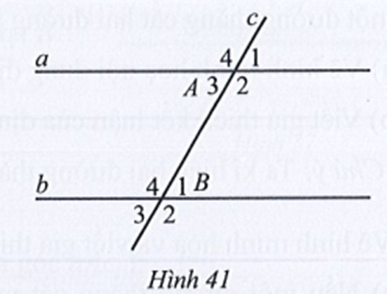
Ta có:

• ${\hat{A}}_{3} = {\hat{A}}_{1} = 60 °$ (hai góc đối đỉnh). Do đó A đúng.

• ${\hat{B}}_{3} = {\hat{B}}_{1} = 60 °$ (hai góc đối đỉnh). Do đó B đúng.

• ${\hat{A}}_{1} + {\hat{A}}_{4} = 180 °$ (hai góc kề bù)

Suy ra ${\hat{A}}_{4} = 180 ° - {\hat{A}}_{1} = 180 ° - 60 ° = 120 ° .$

Do đó C đúng.

• ${\hat{B}}_{3} + {\hat{B}}_{2} = 180 °$ (hai góc kề bù)

Suy ra ${\hat{B}}_{2} = 180 ° - {\hat{B}}_{3} = 180 ° - 60 ° = 120 ° .$

Do đó D sai.

Vậy ta chọn phương án D.

Câu 4

Quan sát Hình 42. Tổng số đo hai góc A₁ và B₁ là:

A. 110°;

B. 240°;

C. 180°;

D. 220°.

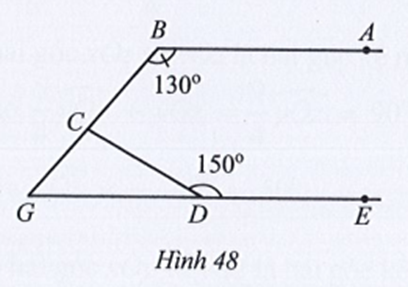
Lời giải

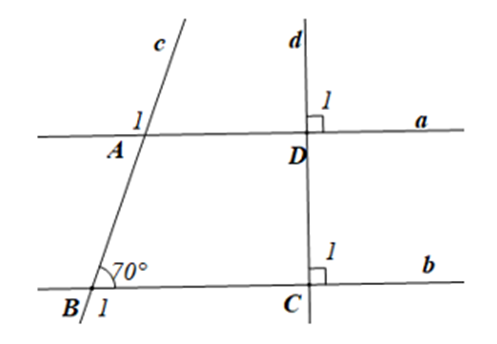
Quan sát Hình 42. Tổng số đo hai góc A1 và B1 là: (ảnh 2)

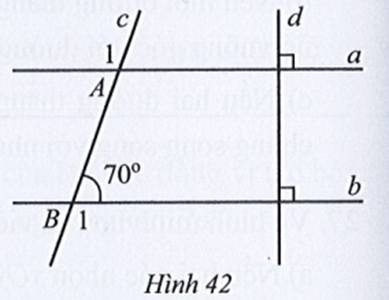
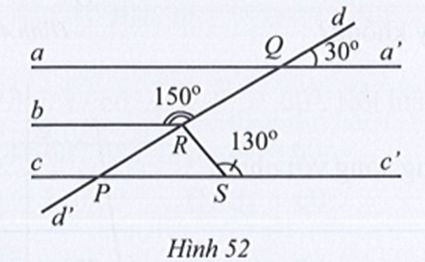
Vì $\hat{A B C}$ và ${\hat{B}}_{1}$ là hai góc kề bù nên ta có:

$\hat{A B C} + {\hat{B}}_{1} = 180 °$

Suy ra ${\hat{B}}_{1} = 180 ° - \hat{A B C} = 180 ° - 70 ° = 110 ° .$

Giả sử d cắt a và b lần lượt tại D và C sao cho ${\hat{D}}_{1} = 90 °, {\hat{C}}_{1} = 90 °$ (hình vẽ).

Do đó ${\hat{D}}_{1} = {\hat{C}}_{1}$ (cùng bằng 90°).

Mà hai D₁ và C₁ ở vị trí đồng vị nên a //b.

Suy ra ${\hat{A}}_{1} = {\hat{B}}_{1}$ (hai góc so le ngoài).

Do đó ${\hat{A}}_{1} = {\hat{B}}_{1} = 110 °$

Nên ${\hat{A}}_{1} + {\hat{B}}_{1} = 110 ° + 110 ° = 220 ° .$

Vậy ta chọn phương án D.

Câu 5

Quan sát Hình 43, biết $\hat{M N O} = \hat{A O B} = \hat{B Q M} = 90 °, \hat{A B O} = 50 ° .$ Tìm số đo mỗi góc NMQ, BMQ, MAN.

Xem đáp án

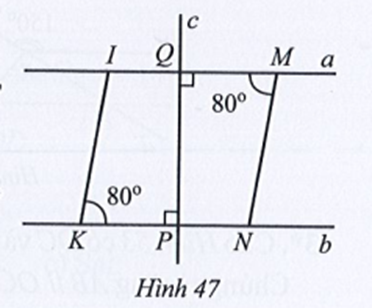
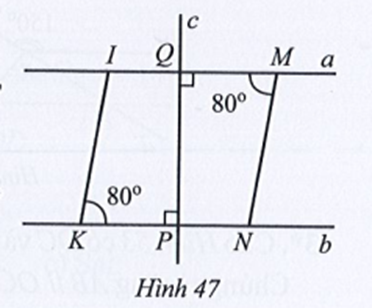
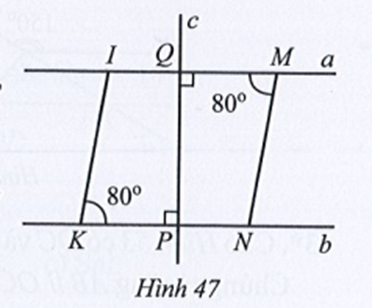
Lời giải

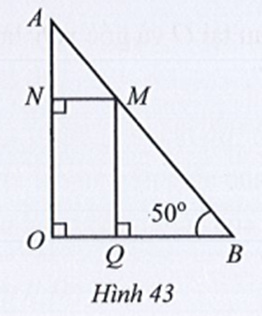
Ta có $\hat{A N M} + \hat{M N O} = 180 °$ (hai góc kề bù)

Suy ra $\hat{A N M} = 180 ° - \hat{M N O} = 180 ° - 90 ° = 90 ° .$

Do đó $\hat{A N M} = \hat{A O B}$ (cùng bằng 90°)

Mà $\hat{A N M}$ và $\hat{A O B}$ ở vị trí đồng vị nên MN // OB.

Suy ra:

• $\hat{N M O} = \hat{B Q M} = 90 °$ (hai góc so le trong)

• $\hat{A M N} = \hat{A B O} = 50 °$ (hai góc đồng vị).

Ta có $\hat{A M N} + \hat{N M Q} = \hat{A M Q}$ (hai góc kề nhau).

Mà $\hat{A M Q} + \hat{B M Q} = 180 °$ (hai góc kề bù).

Do đó $\hat{A M N} + \hat{N M Q} + \hat{B M Q} = 180 °$

Suy ra

$\hat{B M Q} = 180 ° - \hat{A M N} - \hat{N M Q} = 180 ° - 50 ° - 90 ° = 40 ° .$

Ta lại có: $\hat{A O B} = \hat{B Q M}$ (cùng bằng 90°)

Mà $\hat{A O B}$ và $\hat{B Q M}$ ở vị trí đồng vị nên MQ // AO.

Suy ra $\hat{M A N} = \hat{B M Q} = 40 °$ (hai góc đồng vị).

Vậy $\hat{N M O} = 90 °, \hat{B M Q} = 40 °$ và $\hat{M A N} = 40 ° .$

Câu 6

Quan sát Hình 44, biết ME vuông góc với AB tại E và ME, MF lần lượt là tia phân giác của góc AMB và AMC. Vì sao hai đường thẳng MF và AB song song với nhau?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Quan sát Hình 45. Cho OD vuông góc với CC’ tại O, $\hat{A O C} = 160 °, \hat{A O B} - \hat{B O C} = 120 ° .$

a) Tính số đo mỗi góc AOB, BOC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Quan sát Hình 45. Cho OD vuông góc với CC’ tại O,

b) Tia OD có là tia phân giác của góc AOB hay không?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Quan sát Hình 45. Cho OD vuông góc với CC’ tại O, $\hat{A O C} = 160 °, \hat{A O B} - \hat{B O C} = 120 ° .$

c) So sánh hai góc AOC và BOC’.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Quan sát Hình 46, biết Ox vuông góc với Oz và Oy vuông góc với Ot.

a) Hai góc xOt và yOz có bằng nhau hay không?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Quan sát Hình 46, biết Ox vuông góc với Oz và Oy vuông góc với Ot.

b) Chứng tỏ $\hat{x O y} + \hat{z O t} = 180 ° .$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Quan sát Hình 46, biết Ox vuông góc với Oz và Oy vuông góc với Ot.

c) Vẽ tia Ou là tia phân giác của góc tOz. Tia Ou có phải là tia phân giác của góc xOy hay không?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Quan sát Hình 47.

a) Vì sao hai đường thẳng a và b song song với nhau?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

Quan sát Hình 47.

b) Tìm số đo góc MIK.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Quan sát Hình 47.

c) Vì sao hai đường thẳng MN và IK song song với nhau?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

Tìm số đo góc BCD trong Hình 48, biết AB // DE.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Quan sát Hình 49.

Chứng tỏ:

a) yy’ // zz’;

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Quan sát Hình 49.

Chứng tỏ:

b) ut ⊥ zz’;

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Quan sát Hình 49.

Chứng tỏ:

c) xx’ // zz’.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

Quan sát Hình 50, trong đó vết bẩn đã xóa mất đỉnh O của góc xOy. Sử dụng định lí phát biểu trong Bài tập 26b, nêu cách vẽ đường thẳng đi qua điểm M và vuông góc với tia phân giác của góc xOy.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Quan sát Hình 51, biết Ox // HK, tia Ox là tia phân giác của góc yOK. Chứng minh hai góc OHK và OKH bằng nhau.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Tìm số đo góc QRS trong Hình 52, biết aa’ // cc’.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

Cho Hình 53 có OC và DE cùng vuông góc với OD, $\hat{B A O} = 120 °, \hat{A O D} = 150 ° .$ Chứng tỏ rằng AB // OC // DE.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

4.6

312 Đánh giá

50%

40%

Giải SBT Toán 7 Bài tập cuối chương 4 có đáp án

🔥 Đề thi HOT:

Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1

Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2

Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04

15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án

Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01

Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01

Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 3

Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 02

Nội dung liên quan:

Bài tập Góc ở vị trí đặc biệt có đáp án

Giải SBT Toán 7 Bài 1. Góc ở vị trí đặc biệt có đáp án

Giải VBT Toán 7 Cánh diều Bài 1. Góc ở vị trí đặc biệt có đáp án

Bài tập Tia phân giác của một góc có đáp án

Giải SBT Toán 7 Bài 2. Tia phân giác của một góc có đáp án

Giải VBT Toán 7 Cánh diều Bài 2. Tia phân giác của một góc có đáp án

Bài tập Hai đường thẳng song song có đáp án

Giải SBT Toán 7 Bài 3. Hai đường thẳng song song có đáp án

Giải VBT Toán 7 Cánh diều Bài 3. Hai đường thẳng song song có đáp án

Bài tập Định lí có đáp án

Danh sách câu hỏi:

Số đo của góc xOt trong Hình 39 là:

Ở Hình 40 có AB và CD cắt nhau tại O, Ot là tia phân giác của góc BOC, AOC^−BOC^=68°. Số đo góc BOt là:

Cho Hình 41 có A^1=B^3=60°. Kết luận nào sau đây là sai?

Quan sát Hình 42. Tổng số đo hai góc A1 và B1 là:

Quan sát Hình 43, biết MNO^=AOB^=BQM^=90°,ABO^=50°. Tìm số đo mỗi góc NMQ, BMQ, MAN.

Quan sát Hình 44, biết ME vuông góc với AB tại E và ME, MF lần lượt là tia phân giác của góc AMB và AMC. Vì sao hai đường thẳng MF và AB song song với nhau?

Quan sát Hình 45. Cho OD vuông góc với CC’ tại O, AOC^=160°, AOB^−BOC^=120°. a) Tính số đo mỗi góc AOB, BOC.

Quan sát Hình 45. Cho OD vuông góc với CC’ tại O, b) Tia OD có là tia phân giác của góc AOB hay không?

Quan sát Hình 45. Cho OD vuông góc với CC’ tại O, AOC^=160°, AOB^−BOC^=120°. c) So sánh hai góc AOC và BOC’.

Quan sát Hình 46, biết Ox vuông góc với Oz và Oy vuông góc với Ot. a) Hai góc xOt và yOz có bằng nhau hay không?

Quan sát Hình 46, biết Ox vuông góc với Oz và Oy vuông góc với Ot. b) Chứng tỏ xOy^+zOt^=180°.

Quan sát Hình 46, biết Ox vuông góc với Oz và Oy vuông góc với Ot. c) Vẽ tia Ou là tia phân giác của góc tOz. Tia Ou có phải là tia phân giác của góc xOy hay không?

Quan sát Hình 47. a) Vì sao hai đường thẳng a và b song song với nhau?

Quan sát Hình 47. b) Tìm số đo góc MIK.

Quan sát Hình 47. c) Vì sao hai đường thẳng MN và IK song song với nhau?

Tìm số đo góc BCD trong Hình 48, biết AB // DE.

Quan sát Hình 49. Chứng tỏ: a) yy’ // zz’;

Quan sát Hình 49. Chứng tỏ: b) ut ⊥ zz’;

Quan sát Hình 49. Chứng tỏ: c) xx’ // zz’.

Quan sát Hình 50, trong đó vết bẩn đã xóa mất đỉnh O của góc xOy. Sử dụng định lí phát biểu trong Bài tập 26b, nêu cách vẽ đường thẳng đi qua điểm M và vuông góc với tia phân giác của góc xOy.

Quan sát Hình 51, biết Ox // HK, tia Ox là tia phân giác của góc yOK. Chứng minh hai góc OHK và OKH bằng nhau.

Tìm số đo góc QRS trong Hình 52, biết aa’ // cc’.

Cho Hình 53 có OC và DE cùng vuông góc với OD,BAO^=120°,AOD^=150°. Chứng tỏ rằng AB // OC // DE.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Ở Hình 40 có AB và CD cắt nhau tại O, Ot là tia phân giác của góc BOC, $\hat{A O C} - \hat{B O C} = 68 ° .$ Số đo góc BOt là:

Cho Hình 41 có ${\hat{A}}_{1} = {\hat{B}}_{3} = 60 ° .$ Kết luận nào sau đây là sai?

Quan sát Hình 42. Tổng số đo hai góc A₁ và B₁ là:

Quan sát Hình 43, biết $\hat{M N O} = \hat{A O B} = \hat{B Q M} = 90 °, \hat{A B O} = 50 ° .$ Tìm số đo mỗi góc NMQ, BMQ, MAN.

Quan sát Hình 45. Cho OD vuông góc với CC’ tại O, $\hat{A O C} = 160 °, \hat{A O B} - \hat{B O C} = 120 ° .$

a) Tính số đo mỗi góc AOB, BOC.

Quan sát Hình 45. Cho OD vuông góc với CC’ tại O,

b) Tia OD có là tia phân giác của góc AOB hay không?

Quan sát Hình 45. Cho OD vuông góc với CC’ tại O, $\hat{A O C} = 160 °, \hat{A O B} - \hat{B O C} = 120 ° .$

c) So sánh hai góc AOC và BOC’.

Quan sát Hình 46, biết Ox vuông góc với Oz và Oy vuông góc với Ot.

a) Hai góc xOt và yOz có bằng nhau hay không?

Quan sát Hình 46, biết Ox vuông góc với Oz và Oy vuông góc với Ot.

b) Chứng tỏ $\hat{x O y} + \hat{z O t} = 180 ° .$

Quan sát Hình 46, biết Ox vuông góc với Oz và Oy vuông góc với Ot.

c) Vẽ tia Ou là tia phân giác của góc tOz. Tia Ou có phải là tia phân giác của góc xOy hay không?

Quan sát Hình 47.

a) Vì sao hai đường thẳng a và b song song với nhau?

Quan sát Hình 47.

b) Tìm số đo góc MIK.

Quan sát Hình 47.

c) Vì sao hai đường thẳng MN và IK song song với nhau?

Quan sát Hình 49.

Chứng tỏ:

a) yy’ // zz’;

Quan sát Hình 49.

Chứng tỏ:

b) ut ⊥ zz’;

Quan sát Hình 49.

Chứng tỏ:

c) xx’ // zz’.

Cho Hình 53 có OC và DE cùng vuông góc với OD, $\hat{B A O} = 120 °, \hat{A O D} = 150 ° .$ Chứng tỏ rằng AB // OC // DE.