Cho số phức z thõa mãn |z - 1 + i| = 2. Tìm giá trị lớn nhất của biểu thức P = |z + 2 - i|2 + |z - 2 - 3i|2. A.38+810; B.38+1010; C.38+610; D.38+410.

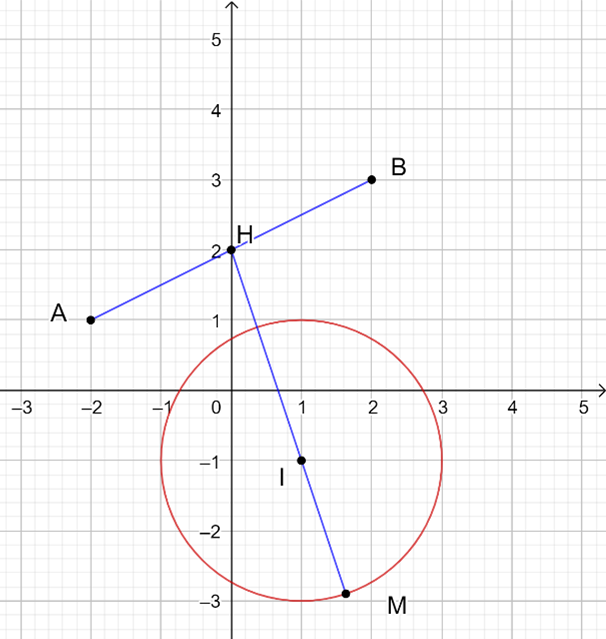
Đáp án đúng là: A Đặt z = a + bi với M(a; b) là điểm biểu diễn của z +) |z - 1 + i| = 2 ⇔a−12+b+12=2 Þ MI = 2 với I(1; -1) Tương tự ta xét P = |z + 2 - i|2 + |z - 2 - 3i|2 = MA2 + MB2 với A(-2; 1) và B(2; 3) Yêu cầu bài toán trở thành tìm giá trị lớn nhất của P với M là điểm thỏa mãn MI = 2 Nên suy ra M thuộc đường tròn tâm I bán kính R = 2 Û (a - 1)2 + (b + 1)2 = 4 Û a2 - 2a + b2 + 2b - 2 = 0 Vậy = (a + 2)2 + (b - 1)2 + (a - 2)2 + (b - 3)2 = 2a2 + 2b2 - 8b + 18 = 2a2 + (2b2 - 8b + 8) + 10 = 2a2 + 2(b - 2)2 + 10 = 2MH2 + 10 Vậy M là điểm thuộc đường tròn tâm I bán kính bằng 2 sao cho 2MH2 + 10 đạt GTLN hay MH lớn nhất với H(0; 2) Từ đó M là giao của đường tròn và đường thẳng HI và M xa AB nhất ⇒MH=MI+IH=2+10 Vậy suy ra Pmax=2MH2+10 =2.2+102+10=38+810.

Cho số phức z thõa mãn |z - 1 + i| = 2. Tìm giá trị lớn nhất của biểu thức P

Hỏi bài tập

🔥 Đề thi HOT:

609 người thi tuần này

53 câu Bài tập về Tính đơn điệu của hàm số có lời giải (P1)

26 câu hỏi 75.7 K lượt thi
544 người thi tuần này

7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)

304 câu hỏi 37.5 K lượt thi
477 người thi tuần này

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

126 câu hỏi 36.2 K lượt thi
442 người thi tuần này

200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P1)

20 câu hỏi 36 K lượt thi
398 người thi tuần này

56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án

56 câu hỏi 4 K lượt thi
388 người thi tuần này

87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án

40 câu hỏi 4.9 K lượt thi
388 người thi tuần này

79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án

40 câu hỏi 4.9 K lượt thi
382 người thi tuần này

20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)

20 câu hỏi 5.6 K lượt thi

Đăng ký gói thi VIP

VIP +3 tháng ( 199,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +6 tháng ( 299,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Siêu tiết kiệm - Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

Cho số phức z thõa mãn |z - 1 + i| = 2. Tìm giá trị lớn nhất của biểu thức P = |z + 2 - i|² + |z - 2 - 3i|².

Nhà sách VIETJACK:

Tìm họ nguyên hàm của hàm số $f (x) = \frac{1}{1 - 2 x}$ trên khoảng $(\frac{1}{2}; + \infty) .$

Trong không gian Oxyz, đường thẳng d đi qua điểm A(1; −2; 1) và vuông góc với mặt phẳng (P): x - 2y + 3z - 1 = 0 có phương trình là

Cho $F (x) = \frac{1}{2 x^{2}}$ là một nguyên hàm của hàm số $\frac{f (x)}{x}$ . Tìm họ nguyên hàm của hàm số $f^{'} (x) \ln x .$

Trong không gian Oxyz, đường thẳng $d : \frac{x - 1}{2} = \frac{y}{- 3} = \frac{z + 2}{1}$ đi qua điểm nào dưới đây?

Trong không gian Oxyz, cho mặt cầu (S): x² + y² + z² + 2x - 4y + 2z - 3 = 0. Viết phương trình mặt phẳng (a) chứa trục Oz cắt mặt cầu (S) theo thiết diện là đường tròn có chu vi bằng 6p.

Cho hàm số y = f (x) có đạo hàm liên tục trên ℝ thỏa mãn $f (x) + f (\frac{π}{2} - x) = \sin x . \cos x,$ với mọi x Î ℝ và f (0) = 0. Tính $\int_{0}^{\frac{π}{2}} x . f' (x) d x .$

Trong không gian Oxyz, cho ba điểm A(1; -2; 1), B(-1; 3; 3), C(0; −3; 1). Một véctơ pháp tuyến của mặt phẳng (ABC) là

Bình luận

🔥 Đề thi HOT:

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

Cho số phức z thõa mãn |z - 1 + i| = 2. Tìm giá trị lớn nhất của biểu thức P = |z + 2 - i|2 + |z - 2 - 3i|2.

Nhà sách VIETJACK:

Tìm họ nguyên hàm của hàm số fx=11−2x trên khoảng 12;+∞.

Trong không gian Oxyz, đường thẳng d đi qua điểm A(1; −2; 1) và vuông góc với mặt phẳng (P): x - 2y + 3z - 1 = 0 có phương trình là

Cho Fx=12x2 là một nguyên hàm của hàm số fxx . Tìm họ nguyên hàm của hàm số f'xlnx.

Trong không gian Oxyz, đường thẳng d:x−12=y−3=z+21 đi qua điểm nào dưới đây?

Trong không gian Oxyz, cho mặt cầu (S): x2 + y2 + z2 + 2x - 4y + 2z - 3 = 0. Viết phương trình mặt phẳng (a) chứa trục Oz cắt mặt cầu (S) theo thiết diện là đường tròn có chu vi bằng 6p.

Cho hàm số y = f (x) có đạo hàm liên tục trên ℝ thỏa mãn fx+fπ2−x=sinx.cosx, với mọi x Î ℝ và f (0) = 0. Tính ∫0π2x.f'xdx.

Trong không gian Oxyz, cho ba điểm A(1; -2; 1), B(-1; 3; 3), C(0; −3; 1). Một véctơ pháp tuyến của mặt phẳng (ABC) là

Bình luận

🔥 Đề thi HOT:

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho số phức z thõa mãn |z - 1 + i| = 2. Tìm giá trị lớn nhất của biểu thức P = |z + 2 - i|² + |z - 2 - 3i|².

Tìm họ nguyên hàm của hàm số $f (x) = \frac{1}{1 - 2 x}$ trên khoảng $(\frac{1}{2}; + \infty) .$

Cho $F (x) = \frac{1}{2 x^{2}}$ là một nguyên hàm của hàm số $\frac{f (x)}{x}$ . Tìm họ nguyên hàm của hàm số $f^{'} (x) \ln x .$

Trong không gian Oxyz, đường thẳng $d : \frac{x - 1}{2} = \frac{y}{- 3} = \frac{z + 2}{1}$ đi qua điểm nào dưới đây?

Trong không gian Oxyz, cho mặt cầu (S): x² + y² + z² + 2x - 4y + 2z - 3 = 0. Viết phương trình mặt phẳng (a) chứa trục Oz cắt mặt cầu (S) theo thiết diện là đường tròn có chu vi bằng 6p.

Cho hàm số y = f (x) có đạo hàm liên tục trên ℝ thỏa mãn $f (x) + f (\frac{π}{2} - x) = \sin x . \cos x,$ với mọi x Î ℝ và f (0) = 0. Tính $\int_{0}^{\frac{π}{2}} x . f' (x) d x .$