Câu hỏi:

13/07/2024 564

Tìm m để đường thẳng (d): $y = (m - 1) x + \frac{1}{2} m^{2} + m$ đi qua điểm

Chứng minh rằng parabol (P) luôn cắt đường thẳng d tịa hai điểm phân biệt A và B. Gọi $x_{1}; x_{2}$ là hoàng độ hai điểm A, B. Tìm m sao cho $x_{1}^{2} + x_{2}^{2} + 6 x_{1} x_{2} > 2019$

Xem lời giải

Câu hỏi trong đề: Bộ đề Ôn tập Toán 9 thi vào 10 năm 2019 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương trình hoành độ giao điểm của P và d là:

$\frac{1}{2} x^{2} = (m - 1) x + \frac{1}{2} m^{2} + m$ $\Leftrightarrow \frac{1}{2} x^{2} - (m - 1) x - \frac{1}{2} m^{2} - m = 0 (1)$

Ta có

Δ = {[- (m - 1)]}^{2} - 4. \frac{1}{2} . (- \frac{1}{2} m^{2} - m)

Δ = m^{2} - 2 m + 1 + m^{2} + 2 m

Δ = 2 m^{2} + 1 > 0

với mọi m

Suy ra phương trình 1 luôn có hai nghiệm phân biết với mọi m

Nên P luôn cắt d tại hai điểm phân biệt A và B

Theo vi-ét ta có:

\{\begin{matrix} x_{1} + x_{2} = 2 (m - 1) \\ x_{1} . x_{2} = - m^{2} - 2 m \end{matrix}

Theo đề ta có: $x_{1}^{2} + x_{2}^{2} + 6 x_{1} x_{2} > 2019$ $\Leftrightarrow {[2 (m - 1)]}^{2} + 4 (- m^{2} - 2 m) - 2019 > 0$ $\Leftrightarrow 4 m^{2} - 8 m + 4 - 4 m^{2} - 8 m - 2019 > 0$ $\Leftrightarrow - 16 m - 2015 > 0$ $\Leftrightarrow m < \frac{2015}{16}$

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong mặt phẳng tọa độ Oxy , cho parabol (P) có phương trình $y = x^{2}$ và đường thẳng (d) có phương trình $y = 2 (m - 1) x + m + 1$ (với là tham số).

Chứng minh rằng (d) luôn cắt (P) tại hai điểm phân biệt với mọi giá trị của .

Tìm các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ $x_{1}, x_{2}$ thỏa mãn $x_{1} + 3 x_{2} - 8 = 0$ .

Xem đáp án

Lời giải

Phương trình hoành độ giao điểm của và :

$x^{2} = 2 (m - 1) x + m + 1 \Leftrightarrow x^{2} - 2 (m - 1) x - m - 1 = 0$ (1)

Số nghiệm phương trình (1) là số giao điểm của và .

Ta có $Δ' = {(m - 1)}^{2} - (- m - 1) = m^{2} - m + 2$ .

Ta có $m^{2} - m + 2 = {(m - \frac{1}{2})}^{2} + \frac{7}{4} > 0$ với mọi giá trị của .

Suy ra $Δ' > 0$ với mọi giá trị của .

phương trình (1) luôn có hai nghiệm phân biệt với mọi hay luôn cắt tại hai điểm phân biệt.

b) Tìm các giá trị của để cắt tại hai điểm phân biệt có hoành độ $x_{1}, x_{2}$ thỏa mãn $x_{1} + 3 x_{2} - 8 = 0$ .

Theo câu a), ta có là hai nghiệm phương trình (1) nên theo Viet: $\{\begin{cases} x_{1} + x_{2} = 2 (m - 1) = 2 m - 2 \\ x_{1} x_{2} = - m - 1 \end{cases}$

Kết hợp giả thiết ta có $\{\begin{cases} x_{1} + x_{2} = 2 m - 2 (2) \\ x_{1} x_{2} = - m - 1 (3) \\ x_{1} + 3 x_{2} - 8 = 0 (4) \end{cases}$

Từ (2) và (4), tính được $x_{1} = 3 m - 7; x_{2} = - m + 5$

Thay vào (3), tính được $(5 - m) (3 m - 7) = - m - 1 \Leftrightarrow 3 m^{2} - 23 m + 34 = 0 \Leftrightarrow [\begin{array}{l} m = 2 \\ m = \frac{17}{3} \end{array}$ .

Vậy $m = 2; m = \frac{17}{3}$ thỏa mãn đề bài.

Câu 2

Trong mặt phẳng tọa độ $(O x y)$ , cho parabol (P): $y = \frac{1}{2} x^{2}$ và đường thẳng (d): $y = (2 m - 1) x + 5$ .

a) Vẽ đồ thị của (P).

b) Tìm m để đường thẳng (d) đi qua điểm $E (7; 12)$ .

c) Đường thẳng cắt parabol (P) tại hai điểm A, B. Tìm tọa độ của A, B và tính diện tích tam giác OAB.

Xem đáp án

Lời giải

Bảng giá trị :

x	-2	-1	0	1	2
x²	2	1/2	0	1/2	2

Đồ thị

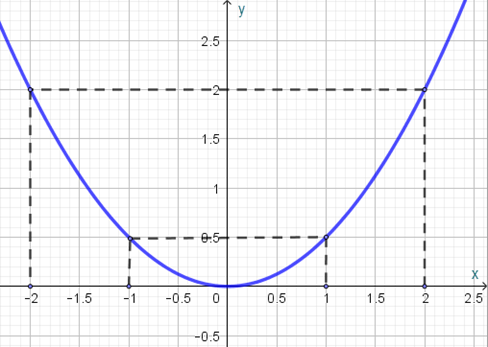
b) Đường thẳng (d): $y = (2 m - 1) x + 5$ đi qua điểm $E (7; 12)$ , ta có $12 = (2 m - 1) .7 + 5$

$\Leftrightarrow 2 m - 1 = 1 \Leftrightarrow m = 1$

c) Phương trình hoành độ giao điểm của (P) và đường thẳng y = 2 là :

$\frac{1}{2} x^{2} = 2 \Leftrightarrow x^{2} = 4 \Leftrightarrow [\begin{matrix} x = 2 \\ x = - 2 \end{matrix}$

AB = 4, H(0 ;2) là giao điểm của đường thẳng y = 2 và trục tung

Diện tích tam giác OAB : $S_{Δ O A B} = \frac{1}{2} A B . O H = 4$ (đvdt)

Câu 3