Câu hỏi:
13/07/2024 8,304
Cho tam giác ABC vuông tại A. Kẻ đường cao AH của tam giác.
Kẻ \(HM \bot AB\) và \(HN \bot AC\). Chứng minh \(AM.AB = AN.AC\)
Cho tam giác ABC vuông tại A. Kẻ đường cao AH của tam giác.
Kẻ \(HM \bot AB\) và \(HN \bot AC\). Chứng minh \(AM.AB = AN.AC\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
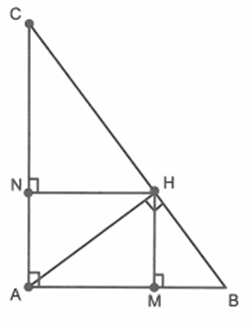
Xét \(\Delta AHM\) và \(\Delta ABH\) có: \(\widehat {MAH}\) chung; \(\widehat {AMH} = \widehat {AHB} = 90^\circ \)
\( \Rightarrow \Delta AHM\~\Delta AHB\) (g.g) \( \Rightarrow \frac{{AH}}{{AB}} = \frac{{AM}}{{AH}} \Rightarrow A{H^2} = AM.AB\) (1)
Xét \(\Delta AHN\) và \(\Delta ABH\) có: \(\widehat {NAH}\) chung; \(\widehat {ANH} = \widehat {AHC} = 90^\circ \)
\( \Rightarrow \Delta AHN\~\Delta ACH\)\[ \Rightarrow \frac{{AH}}{{AC}} = \frac{{AN}}{{AH}} \Rightarrow A{H^2} = AN.AC\] (2)
Từ (1), (2) suy ra: \[AM.AB = AN.AC\]
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
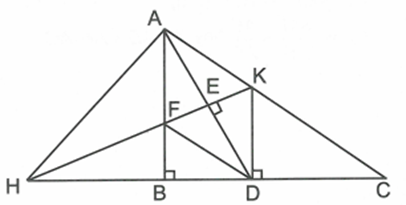
Do AB, DK cùng vuông góc với BC nên \[AB\parallel DK\]. Suy ra \[\widehat {BAD} = \widehat {ADK}\]
Mặt khác, \[\widehat {ADK} = \widehat {KHD}\] (cùng phụ với \[\widehat {HKD}\]). Do đó \[\widehat {BAD} = \widehat {KHD}\]
Xét \[\Delta ABD\] và \[\Delta HDK\] có: \[\widehat {BAD} = \widehat {KHD};\,\,\widehat {ABD} = \widehat {HDK} = 90^\circ \] nên \[\Delta ABD\sim\Delta HDK\] (g.g)
Lời giải
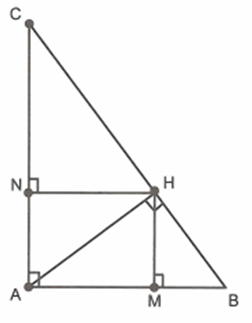
Ta có: \[AM.AB = AN.AC \Rightarrow \frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\]
Xét \[\Delta AMN\] và \[\Delta ABC\] có: \[\widehat {MAN}\] chung; \[\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\] nên \(\Delta AMN\sim\Delta ACB\) (c.g.c)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo