Câu hỏi:
13/07/2024 3,068
Cho tứ giác ABCD có diện tích 36 cm2, trong đó diện tích \[\Delta ABC\] là 11 cm2. Qua điểm B kẻ đường thẳng song song với AC cắt AD ở M, cắt CD ở N. Tính diện tích \[\Delta MND\].
Cho tứ giác ABCD có diện tích 36 cm2, trong đó diện tích \[\Delta ABC\] là 11 cm2. Qua điểm B kẻ đường thẳng song song với AC cắt AD ở M, cắt CD ở N. Tính diện tích \[\Delta MND\].
Quảng cáo
Trả lời:
Giải bởi Vietjack
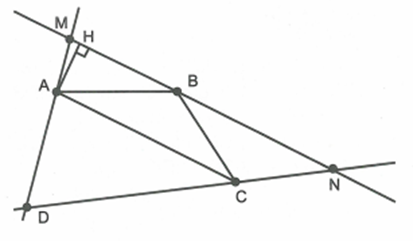
Ta có:
\[{S_{\Delta ADC}} = {S_{ABCD}} - {S_{\Delta ABC}} = 25c{m^2}\]
Dễ dàng chứng minh được \[\Delta DAC\~\Delta DMN\]
Suy ra
\[\frac{{{S_{\Delta ADC}}}}{{{S_{\Delta DMN}}}} = {\left( {\frac{{AC}}{{MN}}} \right)^2} = {k^2}\]
Kẻ \[AH \bot MN\]
Đặt \[{S_{\Delta DMN}} = S,\,\,{S_{\Delta ADC}} = {S_1},\,{S_{ACNM}} = {S_2}\] thì ta có:
\[{S_1} = {k^2}S \Rightarrow S = \frac{{{S_1}}}{{{k^2}}} = \frac{{25}}{{{k^2}}}\]
\[{S_{\Delta ABC}} = \frac{1}{2}AH.AC\]
\[{S_2} = {S_{\Delta AMB}} + {S_{\Delta BCN}} + {S_{\Delta ABC}} = \frac{1}{2}AH.MB + \frac{1}{2}AH.NB + \frac{1}{2}AH.AC\]
\[ = \frac{1}{2}AH(MN + AC) = \frac{1}{2}AH.\left( {\frac{{AC}}{k} + AC} \right) = \frac{{k + 1}}{k}{S_{\Delta ABC}}\]
\[ \Rightarrow {S_2} = \frac{{11(k + 1)}}{k}\]
Mặt khác \[S = {S_1} + {S_2} \Rightarrow \frac{{25}}{{{k^2}}} = 25 + \frac{{11(k + 1)}}{k} \Leftrightarrow 25{k^2} + 11k(k + 1) - 25 = 0 \Leftrightarrow k = \frac{{25}}{{36}}\]
Vậy \[S = 51,84c{m^2}\]
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
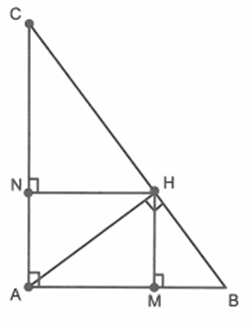
Xét \(\Delta AHM\) và \(\Delta ABH\) có: \(\widehat {MAH}\) chung; \(\widehat {AMH} = \widehat {AHB} = 90^\circ \)
\( \Rightarrow \Delta AHM\~\Delta AHB\) (g.g) \( \Rightarrow \frac{{AH}}{{AB}} = \frac{{AM}}{{AH}} \Rightarrow A{H^2} = AM.AB\) (1)
Xét \(\Delta AHN\) và \(\Delta ABH\) có: \(\widehat {NAH}\) chung; \(\widehat {ANH} = \widehat {AHC} = 90^\circ \)
\( \Rightarrow \Delta AHN\~\Delta ACH\)\[ \Rightarrow \frac{{AH}}{{AC}} = \frac{{AN}}{{AH}} \Rightarrow A{H^2} = AN.AC\] (2)
Từ (1), (2) suy ra: \[AM.AB = AN.AC\]
Lời giải
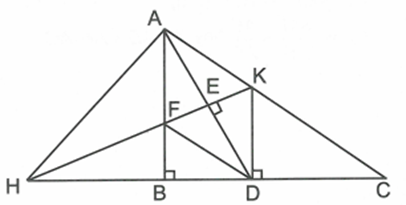
Do AB, DK cùng vuông góc với BC nên \[AB\parallel DK\]. Suy ra \[\widehat {BAD} = \widehat {ADK}\]
Mặt khác, \[\widehat {ADK} = \widehat {KHD}\] (cùng phụ với \[\widehat {HKD}\]). Do đó \[\widehat {BAD} = \widehat {KHD}\]
Xét \[\Delta ABD\] và \[\Delta HDK\] có: \[\widehat {BAD} = \widehat {KHD};\,\,\widehat {ABD} = \widehat {HDK} = 90^\circ \] nên \[\Delta ABD\sim\Delta HDK\] (g.g)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận