Chủ đề 2: Tam giác đồng dạng có đáp án

26 người thi tuần này 4.6 2.9 K lượt thi 48 câu hỏi 30 phút

Câu 1/48

Cho tam giác ABC có \[AB = 6cm,\,AC = 9cm,\,BC = 12cm\] và \[\Delta MNP\] có \[MN = 24cm,\,NP = 18cm,\,MP = 12cm\].

Chứng minh \[\Delta ABC \sim \Delta MNP\].

Xem đáp án

Lời giải

Ta có: \[\frac{{AB}}{{MP}} = \frac{{AC}}{{NP}} = \frac{{BC}}{{MN}} = \frac{1}{2}\] nên \[\Delta ABC \sim \Delta PMN\] (c.c.c).

Câu 2/48

Cho tam giác ABC có \[AB = 6cm,\,AC = 9cm,\,BC = 12cm\] và \[\Delta MNP\] có \[MN = 24cm,\,NP = 18cm,\,MP = 12cm\].

Tính tỉ số diện tích của hai tam giác trên.

Xem đáp án

Lời giải

Do \[\Delta ABC \sim \Delta PMN\] nên \[\frac{{{S_{\Delta ABC}}}}{{{S_{\Delta MNP}}}} = {\left( {\frac{{AB}}{{MP}}} \right)^2} = \frac{1}{4}\].

Câu 3/48

Cho tam giác ABC vuông tại A, đường cao AH. Biết \[AB = 4cm,\,AC = 3cm\].

Chứng minh \[\Delta HAC\sim\Delta ABC\].

Xem đáp án

Lời giải

Xét \[\Delta HAC\] và \[\Delta ABC\] có: \[\widehat {BAC} = \widehat {AHC} = 90^\circ ;\,\,\widehat C\] chung nên \[\Delta HAC\sim\Delta ABC\] (g.g).

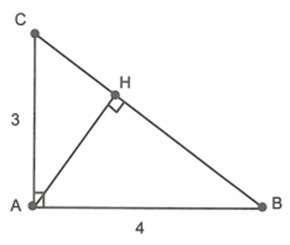
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 4cm, AC = 3 cm (ảnh 1)

Câu 4/48

Cho tam giác ABC vuông tại A, đường cao AH. Biết \[AB = 4cm,\,AC = 3cm\].

Tính độ dài CH.

Xem đáp án

Lời giải

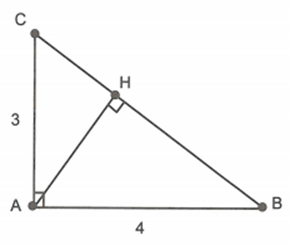
Cho tam giác ABC vuông tại A, đường cao AH. Tính độ dài CH. (ảnh 1)

Áp dụng định lí Pitago cho tam giác vuông ABC ta dễ dàng tính được \[BC = 5cm\].

Do \[\Delta HAC\~\Delta ABC\] nên

\[\frac{{CH}}{{CA}} = \frac{{AC}}{{BC}} \Rightarrow \frac{{CH}}{3} = \frac{3}{5} \Rightarrow CH = 1,8cm\]

Câu 5/48

Cho hình thang ABCD \[(AB\parallel CD)\] có \[\widehat {DAB} = \widehat {DBC}\] và \[AD = 5cm,\,AB = 3cm,\,BC = 9cm\].

Chứng minh \[\Delta DAB\sim\Delta CBD\].

Xem đáp án

Lời giải

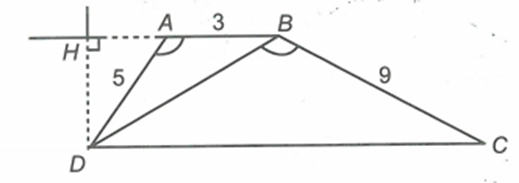
Cho hình thang ABCD (AB // CD) có góc DAB = góc DBC và AD = 5 cm (ảnh 1)

\[AB\parallel CD \Rightarrow \widehat {ABD} = \widehat {BDC}\].

Xét \[\Delta DAB\] và \[\Delta CBD\] có: \[\widehat {DAB} = \widehat {DBC};\,\widehat {ABD} = \widehat {BDC}\] nên \[\Delta DAB\sim\Delta CBD\] (g.g).

Câu 6/48

Cho hình thang ABCD \[(AB\parallel CD)\] có \[\widehat {DAB} = \widehat {DBC}\] và \[AD = 5cm,\,AB = 3cm,\,BC = 9cm\]

Từ câu a, tính độ dài DB, DC.

Xem đáp án

Lời giải

Cho hình thang ABCD. Từ bài trên, tính độ dài DB, DC. (ảnh 1)

\[\Delta DAB\~\Delta CBD \Rightarrow \frac{{DA}}{{CB}} = \frac{{AB}}{{BD}} = \frac{{DB}}{{CD}} \Rightarrow \frac{5}{9} = \frac{3}{{BD}} = \frac{{BD}}{{CD}} \Rightarrow BD = 5,4cm;\,CD = 9,72cm\].

Câu 7/48

Cho hình thang ABCD \[(AB\parallel CD)\] có \[\widehat {DAB} = \widehat {DBC}\] và \[AD = 5cm,\,AB = 3cm,\,BC = 9cm\]

Tính diện tích hình thang ABCD, biết diện tích tam giác ABD bằng 5cm²

Xem đáp án

Lời giải

Cho hình thang ABCD. Tính diện tích hình thang ABCD, biết diện tích tam giác ABD (ảnh 1)

Kẻ DH vuông góc với AB tại H

Theo giả thiết: \[{S_{ABD}} = 5 \Rightarrow \frac{1}{2}DH.AB = 5 \Rightarrow DH = \frac{{10}}{3}cm\].

Từ đó: \[{S_{ABCD}} = \frac{1}{2}DH(AB + CD) = \frac{1}{2}.\frac{{10}}{3}(3 + 9,72) = \frac{{106}}{5}c{m^2}\]

Câu 8/48

Cho \[DE\parallel BC\], D là một điểm trên cạnh AB, E là một điểm trên cạnh AC sao cho \[DE\parallel BC\]. Xác định vị trí của điểm D sao cho chu vi tam giác ADE bằng \[\frac{2}{5}\] chu vi tam giác ABC. Tính chu vi của hai tam giác đó, biết tổng 2 chu vi bằng 63cm.

Xem đáp án

Lời giải

Cho DE // BC, D là một điểm trên cạnh AB, E là một điểm trên cạnh AC sao cho (ảnh 1)

Do \[DE\parallel BC\] nên dễ dàng chứng minh được \[\Delta ADE\~\Delta ABC\] (g.g) với tỉ số đồng dạng \[k = \frac{{AD}}{{AB}}\].

Khi đó \[AD = kAB,\,AE = kAC\] và \[DE = kBC\] nên \[C{V_{\Delta ADE}} = k.C{V_{\Delta ABC}}\] (1).

Theo giả thiết chu vi tam giác ADE bằng \[\frac{2}{5}\] chu vi tam giác ABC suy ra \[k = \frac{2}{5}\].

Vậy \[AD = \frac{2}{5}AB\].

Từ (1) suy ra \[\frac{{C{V_{\Delta ADE}}}}{k} = \frac{{C{V_{\Delta ABC}}}}{1} = \frac{{C{V_{\Delta ADE}} + C{V_{\Delta ABC}}}}{{1 + k}} = \frac{{63}}{{1 + \frac{2}{5}}} = 45\]

\[ \Rightarrow C{V_{\Delta ADE}} = 18cm,\,\,C{V_{\Delta ABC}} = 45cm\]

Câu 9/48