Chủ đề 1: Định lí Ta-lét có đáp án

58 người thi tuần này 4.6 2.6 K lượt thi 18 câu hỏi 30 phút

Câu 1

Cho đoạn thẳng \(AB = 15cm\), M là một điểm trên đoạn thẳng AB sao cho \(\frac{{MA}}{{MB}} = \frac{7}{4}\). Tính độ dài MA và MB.

Xem đáp án

Lời giải

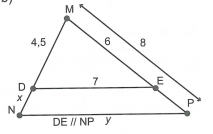
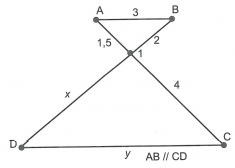
Theo giả thiết, \(\frac{{MA}}{{MB}} = \frac{7}{4} \Rightarrow \frac{{MA}}{7} = \frac{{MB}}{4} = \frac{{MA + MB}}{{7 + 4}} = \frac{{AB}}{{11}} = \frac{{15}}{{11}}\)

\( \Rightarrow MA \approx 9,55cm;\,\,MB \approx 5,45cm\)

Câu 2

Tính độ dài x trong các hình sau:

Xem đáp án

Lời giải

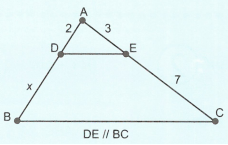
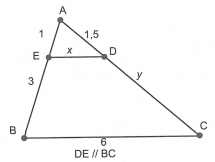
Do \(DE\parallel BC\) nên theo định lí Ta-lét ta có: \(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}} \Rightarrow \frac{2}{x} = \frac{3}{7} \Rightarrow x = \frac{{14}}{3}\).

Câu 3

Tính độ dài x trong các hình sau:

Xem đáp án

Lời giải

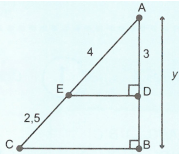
Do \(DE \bot AB,\,\,BC \bot AB\) nên \(DE\parallel BC\).

Từ đó, theo định lí Ta-lét ta có: \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} \Rightarrow \frac{3}{y} = \frac{4}{{4 + 2,5}} \Rightarrow y = 4,875\).

Ví dụ 3: Cho tam giác ABC có \(BC = 15cm\). Trên đường cao AH lấy các điểm I, K sao cho \(AK = KI = IH\). Qua I và K vẽ các đường thẳng EF, MN song song với BC (\(E,M \in AB;F,N \in AC\)). Tính độ dài các đoạn thẳng MN và EF.

Câu 4

Cho tam giác ABC có \(BC = 15cm\). Trên đường cao AH lấy các điểm I, K sao cho \(AK = KI = IH\). Qua I và K vẽ các đường thẳng EF, MN song song với BC (\(E,M \in AB;F,N \in AC\)). Tính độ dài các đoạn thẳng MN và EF.

Xem đáp án

Lời giải

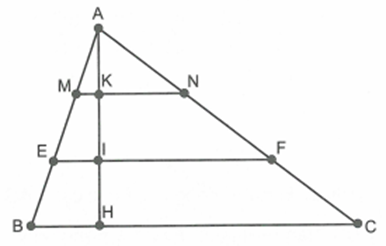
Cho tam giác ABC có BC = 15cm. Trên đường cao AH lấy các điểm I, K sao cho AK = KI (ảnh 1)

\(MK\parallel BH\) nên theo định lí Ta-lét ta có:

\(\frac{{AM}}{{AB}} = \frac{{AK}}{{AH}} = \frac{1}{3}\).

Lại có \(MN\parallel BC\) nên theo định lí Ta-lét ta có:

\(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}} = \frac{1}{3} \Rightarrow MN = 5cm\).

\(EI\parallel BH\) nên theo định lí Ta-lét ta có:

\(\frac{{AE}}{{AB}} = \frac{{AI}}{{AH}} = \frac{2}{3}\).

\({\rm{EF}}\parallel BC\) nên theo định lí Ta-lét ta có: \(\frac{{{\rm{EF}}}}{{BC}} = \frac{{AE}}{{AB}} = \frac{2}{3} \Rightarrow {\rm{EF}} = 10cm\).

Câu 5

Cho tam giác ABC, từ điểm D trên cạnh BC kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AB và AC theo thứ tự tại E và F.

Chứng minh rằng: \(\frac{{AE}}{{AB}} + \frac{{{\rm{AF}}}}{{AC}} = 1\).

Xem đáp án

Lời giải

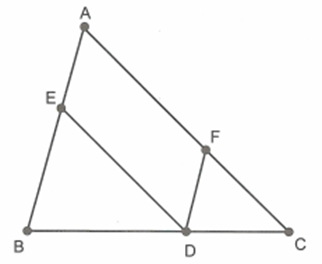
Cho tam giác ABC, từ điểm D trên cạnh BC kẻ các đường thẳng song song với (ảnh 1)

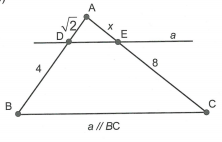
Để chứng minh đẳng thức \(\frac{{AE}}{{AB}} + \frac{{{\rm{AF}}}}{{AC}} = 1\), ta sẽ tìm từng tỉ số

\(\frac{{AE}}{{AB}},\frac{{{\rm{AF}}}}{{AC}}\).

Do \(DE\parallel AC\) nên theo định lí Ta-lét ta có: \(\frac{{AE}}{{AB}} = \frac{{DC}}{{BC}}\) (1).

Do \(DF\parallel AB\) nên theo định lí Ta-lét ta có:

\(\frac{{{\rm{AF}}}}{{AC}} = \frac{{BD}}{{BC}}\) (2)

Cộng vế với vế của (1) và (2) ta được:

\(\frac{{AE}}{{AB}} + \frac{{{\rm{AF}}}}{{AC}} = \frac{{DC}}{{BC}} + \frac{{BD}}{{BC}} = 1\) (đpcm).

Câu 6