Quảng cáo
Trả lời:
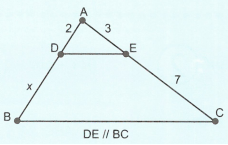
Do \(DE\parallel BC\) nên theo định lí Ta-lét ta có: \(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}} \Rightarrow \frac{2}{x} = \frac{3}{7} \Rightarrow x = \frac{{14}}{3}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
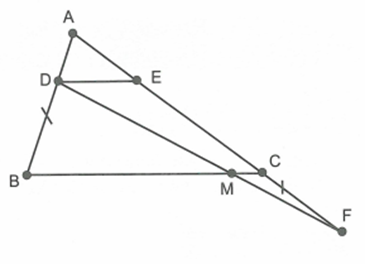
\[DE\parallel CM\] nên theo định lí Ta-lét ta có: \[\frac{{MD}}{{MF}} = \frac{{CE}}{{CF}}\].
Mà \[CF = BD\] nên \[\frac{{MD}}{{MF}} = \frac{{CE}}{{BD}}\] (1).
Lại có, do \[DE\parallel BC\] nên theo định lí Ta-lét ta có:
\[\frac{{AB}}{{BD}} = \frac{{AC}}{{CE}} \Rightarrow \frac{{CE}}{{BD}} = \frac{{AC}}{{AB}}\] (2) .
Từ (1) và (2) ta suy ra \[\frac{{MD}}{{MF}} = \frac{{AC}}{{AB}}\].
Lời giải
Để chứng minh \(\frac{{AB}}{{AE}} + \frac{{AD}}{{{\rm{AF}}}} = \frac{{AC}}{{AI}}\), ta sẽ tìm từng tỉ số \(\frac{{AB}}{{AE}},\frac{{AD}}{{{\rm{AF}}}}\).
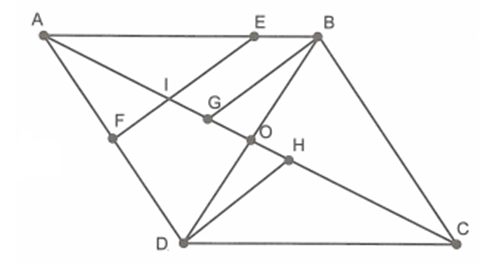
Kẻ \(BG\parallel {\rm{EF(G}} \in {\rm{AC),}}\,\,{\rm{DH}}\parallel {\rm{EF(H}} \in {\rm{AC)}}\).
Gọi O là giao điểm của BD và AC.
Khi đó, theo định lí Ta-lét ta có:
\(\frac{{AB}}{{AE}} = \frac{{AG}}{{AI}};\frac{{AD}}{{{\rm{AF}}}} = \frac{{AH}}{{AI}}\).
\( \Rightarrow \frac{{AB}}{{AE}} + \frac{{AD}}{{{\rm{AF}}}} = \frac{{AG}}{{AI}} + \frac{{AH}}{{AI}} = \frac{{AG + AH}}{{AI}} = \frac{{2AG + GH}}{{AI}}\)
Do \(BG,\,\,DH\parallel E{\rm{F}}\) nên \({\rm{BG}}\parallel {\rm{DH}} \Rightarrow \widehat {GBO} = \widehat {HDO}\). Từ đó \(\Delta BGO = \Delta DHO\) (g.c.g).
Suy ra \(GO = OH \Rightarrow 2AG + GH = 2AG + 2GO = 2AO = AC\)
Do đó, \(\frac{{AB}}{{AE}} + \frac{{AD}}{{{\rm{AF}}}} = \frac{{AC}}{{AI}}\) (đpcm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.