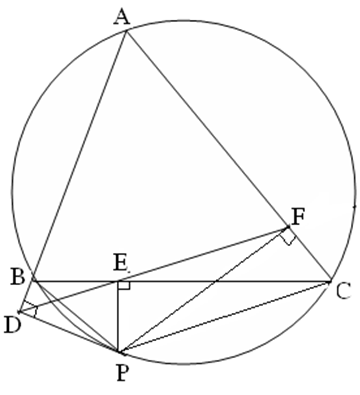
Từ một điểm trên đường tròn ngoại tiếp của một tam giác bất kì hạ các đường vuông góc xuống ba cạnh của tam giác ABC nội tiếp đường tròn. Chứng minh rằng chân của ba đường vuông góc đó thẳng hàng
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì => tứ giác BDPE là tứ giác nội tiếp
(*)(Góc nội tiếp cùng chắn một cung)
=> tứ giác EFCP cũng là tứ giác nội tiếp
(**) (Góc nội tiếp cùng chắn một cung)
Vì tứ giác ABPC nội tiếp đường tròn (1)
(2)
Từ (1) và (2)
(***)
Từ (*) ; (**) và (***)
= D ; E ; F thẳng hàng.
Cách giải 2:
Tứ giác EFCP là tứ giác nội tiếp (1)
Vì tứ giác ABPC nội tiếp đường tròn
Mà (2)
Tứ giác EPDB là tứ giác nội tiếp => ( 3)
Từ (1) ; (2) và (3) ta có :
Suy ra ba điểm D ; E ; F thẳng hàng
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
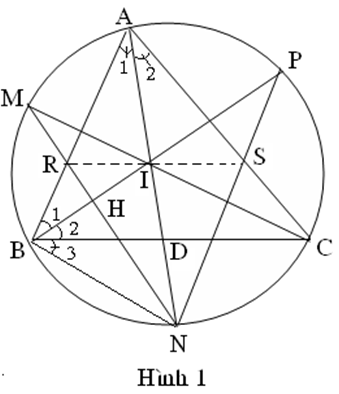
Do đó
(Góc ngoài của tam giác ABI)
=> NBI cân tại N => N thuộc trung trực của đoạn thẳng BI.
Ta chứng minh đường trung trực của đoạn thẳng này chính là RN.
Gọi H là giao điểm của MN và PB. Ta có :
Vì là góc có đỉnh nằm bên trong đường tròn và
=> RN là trung trực của đoạn thẳng BI => BR = RI
=> RBI cân tại R
=> IR // BC (Vì tạo với các tuyến BI hai góc so le trong bằng nhau)
Cũng chứng minh tương tự ta cũng được IS // BC, từ điểm I ở ngoài đường thẳng BC ta chỉ có thể kẻ được một đường thẳng song song với BC
=> R ; I ; S thẳng hàng.
Vậy RS // BC và RS đi qua tâm I của đường tròn nội tiếp tam giác ABC.
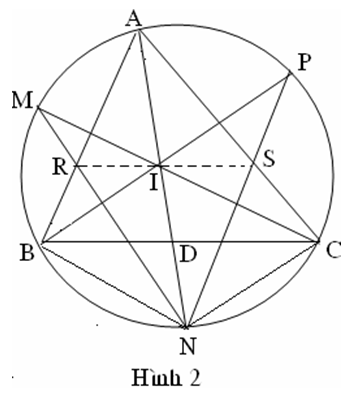
Áp dụng tính chất đường phân giác trong tam giác ABN ta có: (1)
Tương tự: NP là phân giác của tam giác ACN => (2)
vì nên BN = CN kết hợp với (1) và (2) ta được
=> RS // BC (định lý Ta-lét đảo)
Gọi giao điểm của RS với AN là I, của BC và AN là D vì RS // BC nên ta có:
mà suy ra
BND ANB (vì có góc chung và )
Nên . Vậy
Suy ra BI là phân giác của góc
Ở trên ta có I thuộc phân giác AN của ta lại vừa chứng minh I thuộc phân giác nên I là tâm của đường tròn nội tiếp tam giác ABC.( Đpcm)
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập