Dạng 3: Chứng minh ba điểm thẳng hàng có đáp án

🔥 Học sinh cũng đã học

84 người thi tuần này

Đề KSCL Toán 9 tháng 10 năm 2026-2027 Trường THCS Từ Liêm 1 (Hà Nội) có đáp án

567 lượt thi 8 câu hỏi

62 người thi tuần này

Đề KSCL Toán 9 tháng 10 năm 2026-2027 Trường THCS Kim Giang (Hà Nội) có đáp án

545 lượt thi 8 câu hỏi

39 người thi tuần này

Đề KSCL Toán 9 tháng 9 năm 2026-2027 Xã Đại Thanh (Hà Nội) có đáp án

522 lượt thi 8 câu hỏi

36 người thi tuần này

Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Hồng Vân (Hà Nội) có đáp án

519 lượt thi 9 câu hỏi

39 người thi tuần này

Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Ngô Sĩ Liên (Hà Nội) có đáp án

522 lượt thi 7 câu hỏi

34 người thi tuần này

Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS&THPT Lương Thế Vinh (Hà Nội) có đáp án

517 lượt thi 8 câu hỏi

30 người thi tuần này

Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Yên Hòa (Hà Nội) có đáp án

513 lượt thi 8 câu hỏi

36 người thi tuần này

Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Giảng Võ (Hà Nội) có đáp án

519 lượt thi 10 câu hỏi

Danh sách câu hỏi:

Câu 1/2

Cho tam giác ABC nội tiếp trong một đường tròn (O). M ; N ; P lần lượt là cá điểm chính giữa các cung nhỏ $\hat{A B}; \hat{B C}; \hat{C A}$ . MN và NP cắt AB và AC theo thứ tự ở R và S. Chứng minh rằng: RS // BC và RS đi qua tâm của đường tròn nội tiếp tam giác ABC.

Xem đáp án

Lời giải

Cách giải 1: (Hình 1)

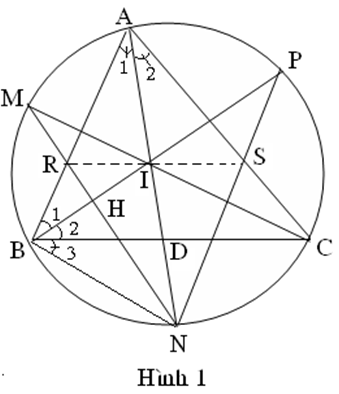
Cho tam giác ABC nội tiếp trong một đường tròn (O). M ; N ; P lần lượt là cá điểm chính giữa các cung nhỏ (ảnh 1)

Xét

△

NBI ta có:

\hat{I B N} = \hat{B_{2}} + \hat{B_{3}}

mà

\hat{B_{2}} = \frac{\hat{C P}}{2}; \hat{B_{3}} = \hat{N A C}

(Góc nội tiếp chắn cung

\hat{N C}

);

\hat{N A C} = \frac{\hat{B A C}}{2}

Do đó

\hat{I B N} = \frac{\hat{A} + \hat{B}}{2}

$\hat{B I N} = \hat{A_{1}} + \hat{B_{1}} = \frac{\hat{A} + \hat{B}}{2}$ (Góc ngoài của tam giác ABI)
$\Rightarrow \hat{I B N} = \hat{B I N}$ => $△$ NBI cân tại N => N thuộc trung trực của đoạn thẳng BI.
Ta chứng minh đường trung trực của đoạn thẳng này chính là RN.
Gọi H là giao điểm của MN và PB. Ta có :
$\hat{B H N} = \frac{1}{2} sđ (\hat{B N} + \hat{A M} + \hat{A P}) = \frac{1}{2} \frac{sđ \hat{B C} + sđ \hat{A B} + sđ \hat{A C}}{2}$
Vì $\hat{B H N}$ là góc có đỉnh nằm bên trong đường tròn và
$\hat{B N} = \frac{\hat{B C}}{2}; \hat{A M} = \frac{\hat{A B}}{2}; \hat{A P} = \frac{\hat{A C}}{2} \Rightarrow \hat{B H N} = \frac{1}{4} . 360^{\circ} = 90^{\circ}$
=> RN là trung trực của đoạn thẳng BI => BR = RI
=> RBI cân tại R $\hat{B_{1}} = \hat{R I B} mà \hat{B_{1}} = \hat{B_{2}} \Rightarrow \hat{B_{2}} = \hat{RIB}$
=> IR // BC (Vì tạo với các tuyến BI hai góc so le trong bằng nhau)
Cũng chứng minh tương tự ta cũng được IS // BC, từ điểm I ở ngoài đường thẳng BC ta chỉ có thể kẻ được một đường thẳng song song với BC
=> R ; I ; S thẳng hàng.
Vậy RS // BC và RS đi qua tâm I của đường tròn nội tiếp tam giác ABC.

Cách giải 2: (Hình 2)

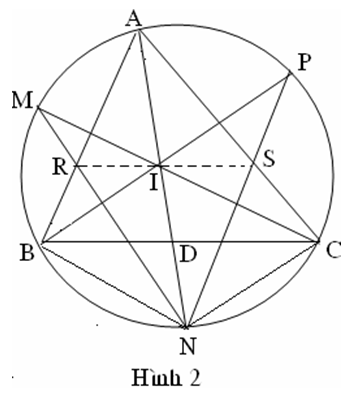
Cho tam giác ABC nội tiếp trong một đường tròn (O). M ; N ; P lần lượt là cá điểm chính giữa các cung nhỏ (ảnh 2)

Theo giả thiết ta có

\hat{M A} = \hat{M B}

do đó MN là phân giác của

\hat{A N B}

Áp dụng tính chất đường phân giác trong tam giác ABN ta có:

\frac{R A}{R B} = \frac{N A}{N B}

(1)
Tương tự: NP là phân giác của tam giác ACN =>

\frac{S A}{S C} = \frac{N A}{N C}

(2)
vì

\hat{B N} = \hat{C N}

nên BN = CN kết hợp với (1) và (2) ta được

\frac{R A}{R B} = \frac{S A}{S C}

=> RS // BC (định lý Ta-lét đảo)
Gọi giao điểm của RS với AN là I, của BC và AN là D vì RS // BC nên ta có:

\frac{A I}{I D} = \frac{R A}{R B}

mà

\frac{N A}{N B} = \frac{R A}{R B}

suy ra

\frac{A I}{I D} = \frac{N A}{N B}

△

BND

~

△

ANB (vì có góc

\hat{B N A}

chung và

\hat{B A N} = \hat{N B D}

)
Nên

\frac{N A}{N B} = \frac{A B}{B D}

. Vậy

\frac{A I}{I D} = \frac{A B}{B D}

Suy ra BI là phân giác của góc

\hat{A B C}

Ở trên ta có I thuộc phân giác AN của

\hat{B A C}

ta lại vừa chứng minh I thuộc phân giác

\hat{A B C}

nên I là tâm của đường tròn nội tiếp tam giác ABC.( Đpcm)

Câu 2/2

Từ một điểm trên đường tròn ngoại tiếp của một tam giác bất kì hạ các đường vuông góc xuống ba cạnh của tam giác ABC nội tiếp đường tròn. Chứng minh rằng chân của ba đường vuông góc đó thẳng hàng

Xem đáp án

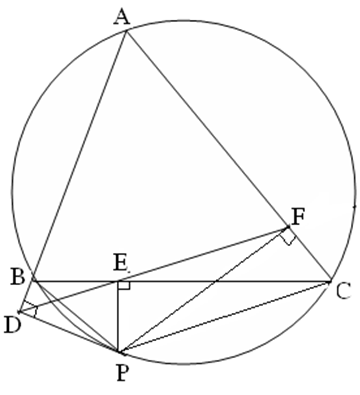
Lời giải

Cách giải 1:
Vì

\hat{D} = \hat{E} = 90^{\circ}

=> tứ giác BDPE là tứ giác nội tiếp

\Rightarrow \hat{B E D} = \hat{B P D}

(*)(Góc nội tiếp cùng chắn một cung)

\hat{F} = \hat{E} = 90^{\circ}

=> tứ giác EFCP cũng là tứ giác nội tiếp

\Rightarrow \hat{F E C} = \hat{F P C}

(**) (Góc nội tiếp cùng chắn một cung)
Vì tứ giác ABPC nội tiếp đường tròn

\Rightarrow \hat{B P C} = π - \hat{A}

(1)

\begin{matrix} P D ⊥ A B \\ P F ⊥ A C \end{matrix}\} \Rightarrow \hat{D P F} = π - \hat{A}

(2)
Từ (1) và (2)

\Rightarrow \hat{B P C} = \hat{D P F}

\Rightarrow \hat{B P D} = \hat{F P C}

(***)
Từ (*) ; (**) và (***)
= D ; E ; F thẳng hàng.

Cách giải 2:

\begin{matrix} P E ⊥ E C \\ P F ⊥ F C \end{matrix}\} \Rightarrow

Tứ giác EFCP là tứ giác nội tiếp

\Rightarrow \hat{F E P} + \hat{P C F} = 180^{\circ}

(1)
Vì tứ giác ABPC nội tiếp đường tròn

\Rightarrow \hat{A B P} + \hat{F C P} = 180^{\circ}

Mà

\hat{A B P} + \hat{B D P} = 180^{\circ} \Rightarrow \hat{F C P} = \hat{D B P}

(2)

\begin{matrix} P D ⊥ B D \\ P E ⊥ B C \end{matrix}\} \Rightarrow

Tứ giác EPDB là tứ giác nội tiếp =>

\hat{D B P} = \hat{D E P}

( 3)
Từ (1) ; (2) và (3) ta có :

\hat{P E F} + \hat{D E P} = 180^{\circ}

Suy ra ba điểm D ; E ; F thẳng hàng

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán