Có một cây tre có độ cao là a. Khi gãy ngọn tre chạm đất ở một khoảng cách là b so với gốc tre. Hãy tìm độ cao chỗ cây tre.
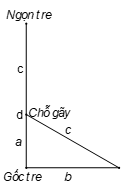
Có một cây tre có độ cao là a. Khi gãy ngọn tre chạm đất ở một khoảng cách là b so với gốc tre. Hãy tìm độ cao chỗ cây tre.

Quảng cáo
Trả lời:
Ta phải tính cạnh a của một tam giác vuông có cạnh bên là b và cạnh huyền là .
Theo định lí Pythagore ta có: .
Từ đây suy ra: .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
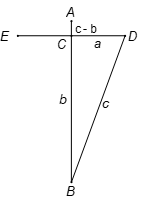
Giả sử chiều rộng của ao là (m), C là trung điểm của ED nên: (m).
Chiều cao cây sậy mặt giữa ao là AB, phần nhô khỏi mặt nước (m).
Mà , giả sử , độ sâu của nước , tam giác BCD là tam giác vuông. Rõ ràng là (m).
Độ dài của AC bằng hiệu giữa đường huyền với cạnh dài của góc vuông.
Vậy bài toán quy về việc tính chiều dài cạnh huyền và cạnh góc vuông lớn của
một tam giác vuông khi biết cạnh góc vuông bé và hiệu giữa cạnh huyền và cạnh góc vuông lớn.
Từ định lí Pythagore, ta có:
.
Vì thế
(1)
(2)
Đem giá trị của a, c-b thay vào hai công thức (1) và (2) sẽ dễ dàng tính được độ sâu của nước là:
(m).
Độ cao của cây sậy là: (m).
Lời giải
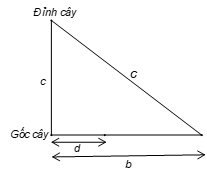
Nếu cây có độ dài thì có bài toán là tính độ dài của cạnh huyền một tam giác vuông có cạnh bên là và . Theo định lí Pythagore ta có:
.
Từ đây suy ra: .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Trường Thiên
Kim mo chi