Câu hỏi:

19/08/2025 43,088

Kim tự tháp Keop – Ai cập có dạng hình chóp đều, đáy là hình vuông, các mặt bên là các tam giác cân chung đỉnh. Mỗi cạnh bên của kim tự tháp dài 214m, cạnh đáy của nó dài 230m.

a) Tính theo mét chiều cao h của kim tự tháp (làm tròn đến số thập phân thứ nhất)

b) Cho biết thể tích của hình chóp được tính theo công thức $V = \frac{1}{3} S . h$ , trong đó S là diện tích mặt đáy, h là chiều cao của hình chóp. Tính theo m³ thể tích của kim tự tháp (làm tròn đến hàng nghìn)

Xem lời giải

Câu hỏi trong đề: Bộ đề Ôn tập Toán 9 thi vào 10 năm 2019 có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

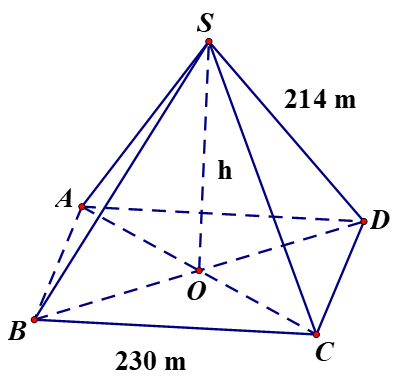
Kim tự tháp Keop – Ai cập có dạng hình chóp đều, đáy là hình vuông, các mặt bên là các tam giác cân chung đỉnh. Mỗi cạnh bên của kim tự tháp dài 214m, cạnh đáy của nó dài 230m. a) Tính theo mét chiều cao h của kim tự tháp (làm tròn đến số thập phân thứ nhất) b) Cho biết thể tích của hình chóp được tính theo công thức , trong đó S là diện tích mặt đáy, h là chiều cao của hình chóp. Tính theo m3 thể tích của kim tự tháp (làm tròn đến hàng nghìn) (ảnh 1)

a) Vì ABCD là hình vuông $\Rightarrow A C = A D \sqrt{2} = 230. \sqrt{2}$

$\Rightarrow A O = \frac{A C}{2} = \frac{230 \sqrt{2}}{2} = 115 \sqrt{2}$

Tam giác SAO vuông tại O nên áp dụng Pytago ta có:

$A O^{2} + S O^{2} = S A^{2}$

$\begin{array}{l} h a y {(115 \sqrt{2})}^{2} + h^{2} = 214^{2} \\ \Rightarrow h = \sqrt{214^{2} - {(115 \sqrt{2})}^{2}} \approx 139,1 \end{array}$

b) T a có diện tích mặt đáy là: $230.230 = 52900 (m^{2})$

Thể tích của kim tự tháp là $V = \frac{1}{3} S h = \frac{1}{3} .52900.139,1 \approx 2453000 (m^{2})$

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho đường tròn (O; R) có đường kính AB vuông góc với dây cung MN tại H (H nằm giữa O và B). Trên tia MN lấy điểm C nằm ngoài đường tròn (O; R) sao cho đoạn thẳng AC cắt đường tròn (O; R) tại điểm K (K khác A), hai dây MN và BK cắt nhau ở E.

a) Chứng minh rằng tứ giác AHEK là tứ giác nội tiếp.

b) Chứng minh: CA.CK = CE.CH.

c) Qua điểm N, kẻ đường thẳng (d) vuông góc với AC, (d) cắt tia MK tại F. Chứng minh tam giác cân.

d) Khi KE = KC. Chứng minh rằng: OK // MN.

Xem đáp án

Lời giải

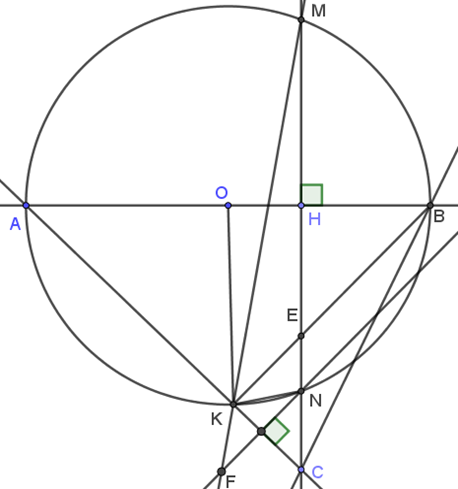
Cho đường tròn (O; R) có đường kính AB vuông góc với dây cung MN tại H (H nằm giữa O và B). Trên tia MN lấy điểm C nằm ngoài đường tròn (O; R) sao cho đoạn thẳng AC cắt đường tròn (O; R) tại điểm K (K khác A), hai dây MN và BK cắt nhau ở E. a) Chứng minh rằng tứ giác AHEK là tứ giác nội tiếp. b) Chứng minh: CA.CK = CE.CH. c) Qua điểm N, kẻ đường thẳng (d) vuông góc với AC, (d) cắt tia MK tại F. Chứng minh tam giác cân. d) Khi KE = KC. Chứng minh rằng: OK // MN. (ảnh 1)

a) Chứng minh rằng tứ giác AHEK là tứ giác nội tiếp.

Ta có : $\hat{A H E} = 90^{0}$

$\hat{A K B} = 90^{0}$ $\Rightarrow \hat{A H E} + \hat{A K B} = 180^{0}$ (1)

Hai góc $\hat{A H E}, \hat{A K B}$ đối nhau (2)

Từ (1), (2) ta có tứ giác AHEK nội tiếp đường tròn đường kính AE.

b) Chứng minh: CA.CK = CE.CH.

Do tứ giác AHEK nội tiếp nên $\hat{H A K} = \hat{K E N}$

vì chung và $\hat{H A K} = \hat{K E N}$ $(\hat{A H C} = \hat{E K C} = 90^{0})$

nên $\frac{C K}{C H} = \frac{CE}{CA} \Leftrightarrow C K . C A = C H . C E$

c)Qua điểm N, kẻ đường thẳng (d) vuông góc với AC, (d) cắt tia MK tại F. Chứng minh tam giác cân.

Do KB // FN nên $\hat{E K N} = \hat{K N F}, \hat{M K B} = \hat{K F N}$ (3)

mà $\hat{M K B} = \hat{E K N}$ (góc nội tiếp cùng chắn cung bằng nhau) (4)

(3), (4) $\Rightarrow \hat{K N F} = \hat{K F N}$ nên tam giác KFN cân tại K.

d) Khi KE = KC. Chứng minh rằng: OK // MN.

Ta có vuông tại K.

mà KE = KC nên tam giác KEC vuông cân tại K $\Rightarrow \hat{K E C} = 45^{0}$

$\hat{O A K} = \hat{O K A} = \hat{K E C} = 45^{0} \Rightarrow \hat{A O K} = 90^{0}$ hay

mà $M N ⊥ A B$ nên OK //MN

Câu 2

Cho tam giác ABC vuông tại A có đường cao AH , biết AB=5cm, BH=3cm . Tính AH, AC và sin CAH.

Xem đáp án

Lời giải

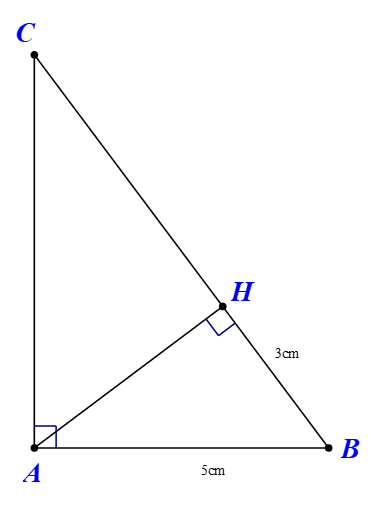
Áp dụng Pitago vào tam giác vuông

$\begin{array}{l} A B^{2} = A H^{2} + B H^{2} \\ \Rightarrow A H^{2} = A B^{2} - B H^{2} = 5^{2} - 3^{2} = 16 \Rightarrow A H = 4 (c m) \end{array}$ .

Áp dụng hệ thức lượng vào tam giác vuông ABC $A H^{2} = B H . C H \Rightarrow C H = \frac{A H^{2}}{B H} = \frac{16}{3} (c m)$

Do đó $B C = B H + C H = 3 + \frac{16}{3} = \frac{25}{3} (c m)$

Áp dụng Pitago vào tam giác vuông ABC $\begin{array}{l} A C^{2} = C H . B C = \frac{16}{3} \cdot \frac{25}{3} = \frac{400}{9} \\ \Rightarrow A C = \frac{20}{3} c m) \end{array}$

$\sin \hat{C A H} = \frac{C H}{C A} = \frac{16}{3} : \frac{20}{3} = \frac{4}{5}$

Cho tam giác ABC vuông tại A có đường cao AH , biết AB=5cm, BH=3cm . Tính AH, AC và sin CAH. (ảnh 1)

Câu 3

Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn đó. Kẻ cát tuyến AMN không đi qua (O) (M nằm giữa A và N). Kẻ hai tiếp tuyến AB, AC với (O;R). (B và C là hai tiếp điểm và C tuộc cung nhỏ MN). Đường thẳng BC cắt MN và AO lần lượt tại E và F. Gọi I là trung điểm của MN.

a) Chứng minh rằng tứ giác ABOC nội tiếp được trong đường tròn.

b) Chứng minh EB.EC = EM.EN và IA là phân giác của $\hat{B I C}$ .

c) Tia MF cắt (O;R) tại điểm thứ hai là D. Chứng minh rằng $Δ A M F ∽ Δ A O N$ và $B C // D N$ .

d) Giả sử OA = 2R. Tính diện tích tam giác ABC theo R.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho đường tròn đường kính AB , các điểm C,D nằm trên đường tròn đó sao cho C,D nằm khác phía đối với đường thẳng AB , đồng thời AD>AC. Gọi điểm chính giữa của các cung nhỏ AC,AD lần lượt là M,N ; giao điểm của MN với AC,AD lần lượt là H,I; giao điểm của MD và CN là K.

a) Chứng minh $\hat{A C N} = \hat{D M N}$ . Từ đó suy ra tứ giác $M C K H$ nội tiếp.

b) Chứng minh $K H$ song song với $A D$ .

c) Tìm hệ thức liên hệ giữa sđ $\overset{⏜}{A C}$ và sđ $\overset{⏜}{A D}$ để song song với $N D$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho điểm S cố định ở bên ngoài đường tròn (O). Vẽ tiếp tuyến SA của đường tròn (O) (với A là tiếp điểm) và cát tuyến SCB không qua tâm O, điểm O nằm trong góc ASB, điểm C nằm giữa S và B. Gọi H là trung điểm của đoạn thẳng CB.

a)      Chứng minh rằng tứ giác SAOH nội tiếp một đường tròn

b)      Chứng mnh rằng $S A^{2} = S B . S C$

c)      Gọi MN là đường kính bất kỳ của đường tròn (O) sao cho ba điểm S, M, N không thẳng hàng. Xác định vị trí của MN để diện tích tam giác SMN lớn nhất

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho tam giác ABC vuông tại A ( AB<AC ), đường cao AH ( H thuộc BC) lấy điểm D sao cho BD=BA , vẽ CE vuông góc với AD ( E thuộc AD)

a)      Chứng minh tứ giác AHCE là tứ giác nội tiếp

b)      Chứng minh $D A . H E = D H . A C$

c)      Chứng minh tam giác EHC cân

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Cho tam giác ABC vuông tại A ( AB<AC ), đường cao AH ( H thuộc BC) lấy điểm D sao cho BD=BA , vẽ CE vuông góc với AD ( E thuộc AD)

a) Chứng minh tứ giác AHCE là tứ giác nội tiếp

b) Chứng minh $D A . H E = D H . A C$

c) Chứng minh tam giác EHC cân