✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

Câu hỏi:

12/07/2024 3,027

Trong một vườn cây có 9 cây. Hãy trồng thành 10 hàng, mỗi hàng có 3 cây.

Xem lời giải

Câu hỏi trong đề: Trắc nghiệm Chuyên đề Toán 9 Chuyên đề 9: Bài toán thực tế Hình học có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Cách 1

Newton đưa ra cách giải như sau:

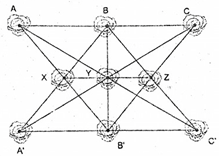
Trong một vườn cây có 9 cây. Hãy trồng thành 10 hàng, mỗi hàng có 3 cây. (ảnh 1)

Các hàng là: $A B C, A Y C^{'}, A X B^{'}, B X A^{'}, B Y B^{'}, B Z C^{'}, C Y A^{'}, C Z B^{'}, X Y Z, A^{'} B^{'} C^{'}$ .

Rõ ràng đây là một cách giải thú vị. ngoài cách giải này, chúng ta có cách giải khác như sau

Cách 2

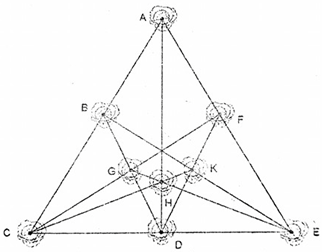
Trong một vườn cây có 9 cây. Hãy trồng thành 10 hàng, mỗi hàng có 3 cây. (ảnh 2)

Các hàng là: $A B C, A F E, A H D, C D E, C H K, C G F, B K E, B G D, F K D, E H G$ .

Bản chất của các cách trồng cây thẳng hàng này như thế nào? Mỗi cách trồng cây có một cơ sở toán học ẩn chứa đằng sau và các cách giải trên không phải ngoại lệ. Tuy nhiên có nhiều cách giải chỉ đưa ra được đáp án mà chưa tìm được cơ sở toán là bản chất của cách trồng cây vì đó là vấn đề rất phức tạp vượt quá khả năng của chúng tôi.

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong một vườn cây có 20 cây. Hãy trồng thành 20 hàng, mỗi hàng có 4 cây.

Xem đáp án

Lời giải

Ta có một cách trồng cây như sau:

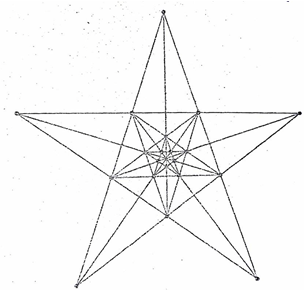
Trong một vườn cây có 20 cây. Hãy trồng thành 20 hàng, mỗi hàng có 4 cây. (ảnh 1)

Câu 2

Cho tam giác ABC với điểm M nằm trong tam giác. Các tia AM, BM, CM cắt các cạnh BC, CA, AB tương ứng tại D, E, F. Gọi K là giao điểm của DE và CM. Gọi H là giao điểm của DF và EM. Chứng minh rằng các đường thẳng $A D, B K, C H$ đồng quy.

Xem đáp án

Lời giải

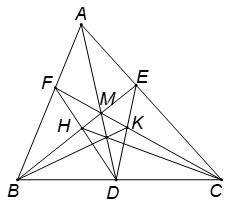
Cho tam giác ABC với điểm M nằm trong tam giác. Các tia AM, BM, CM cắt các cạnh BC, CA, AB tương (ảnh 1)

Áp dụng định lí Ménélaus cho tam giác AMC (với bộ ba điểm thẳng hàng E, K, D) và tam giác BMA (với bộ ba điểm thẳng hàng F, H, D), ta có

$\frac{K M}{K C} . \frac{E C}{E A} . \frac{D A}{D M} = 1, \frac{B H}{H M} . \frac{D M}{D A} . \frac{F A}{F B} = 1$

Suy ra $\frac{K M}{K C} . \frac{E A}{E C} . \frac{D M}{D A}, \frac{B H}{H M} = \frac{F B}{F A} . \frac{D A}{D M}$ (1)

Áp dụng định lí Céva cho tam giác ABC với bộ ba đường thẳng đồng quy $A D, B E, C F$ : $\frac{C D}{B D} . \frac{B F}{F A} . \frac{A E}{E C} = 1$ .

Từ đó: $\frac{C D}{B D} = \frac{F A}{B F} . \frac{E C}{A E}$ (2)

Từ (1) và (2) ta có: $\frac{K M}{K C} . \frac{B H}{H M} . \frac{C D}{B D} = 1$ .

Vậy theo phần đảo của định lí Céva, $B K, C H, M D$ đồng quy, hay $A D, B K, C H$ đồng quy.

Câu 3

Trong một vườn cây có 9 cây. Hãy trồng thành 9 hàng, mỗi hàng có 3 cây.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong một vườn cây có 20 cây. Hãy trồng thành 18 hàng, mỗi hàng có 4 cây.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong một vườn cây có 10 cây. Hãy trồng thành 5 hàng, mỗi hàng có 4 cây.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong một vườn cây có 10 cây. Hãy trồng thành 12 hàng, mỗi hàng có 3 cây.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Vietjack official store

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

🔥 Đề thi HOT:

Bạn vui lòng để lại thông tin để được
TƯ VẤN THÊM

Hoặc gọi Hotline tư vấn: 084 283 45 85
Email: vietjackteam@gmail.com

VietJack