Câu hỏi:

29/10/2022 376

Cho tam giác MNP có ba đường phân giác MA, NB, PC cắt nhau tại I. Vẽ IH vuông góc NP tại H. Khẳng định nào dưới đây là đúng:

A. \(\widehat {NIH} = \widehat {PIH}\);

B. IM = IN = IP;

C. \(\widehat {NIH} = \widehat {PIA}\);

D. IA = IB = IC.

Câu hỏi trong đề: 15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 9: Tính chất ba đường phân giác của tam giác có đáp án (Phần 2) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải

Đáp án đúng là: C

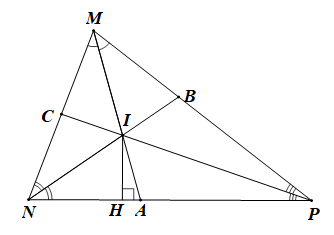
Media VietJack

Xét DMNP có ba đường phân giác MA, NB, PC cắt nhau tại I nên I cách đều ba cạnh của tam giác.

Điểm I không phải là giao điểm ba đường trung trực của tam giác nên không cách đều ba đỉnh. Do đó phương án B, D là sai.

Vì MI là tia phân giác của góc NMP nên \(\widehat {NMI} = \widehat {PMI} = \frac{1}{2}\widehat {PMN}\).

Vì NI là tia phân giác của góc MNP nên \(\widehat {MNI} = \widehat {PNI} = \frac{1}{2}\widehat {MNP}\).

Vì PI là đường phân giác của góc MPN nên \(\widehat {NPI} = \widehat {MPI} = \frac{1}{2}\widehat {MPN}\).

Xét DMIP có \(\widehat {MIP} + \widehat {MPI} + \widehat {PMI} = 180^\circ \) (tổng ba góc trong một tam giác)

Nên \(\widehat {MIP} = 180^\circ - \left( {\widehat {MPI} + \widehat {PMI}} \right)\)

Suy ra \(\widehat {MIP} = 180^\circ - \frac{1}{2}\left( {\widehat {MPN} + \widehat {PMN}} \right)\).

Xét DMNP có \(\widehat {MNP} + \widehat {MPN} + \widehat {PMN} = 180^\circ \)(tổng ba góc trong một tam giác)

Nên \(\widehat {MPN} + \widehat {PMN} = 180^\circ - \widehat {MNP}\).

Do đó \(\widehat {MIP} = 180^\circ - \frac{1}{2}\left( {180^\circ - \widehat {MNP}} \right)\)

Hay \(\widehat {MIP} = 180^\circ - 90^\circ + \frac{1}{2}\widehat {MNP} = 90^\circ + \frac{1}{2}\widehat {MNP}\).

Ta có \(\widehat {MIP} + \widehat {PIA} = 180^\circ \) (hai góc kề bù)

Nên \(\widehat {PIA} = 180^\circ - \widehat {MIP} = 180^\circ - \left( {90^\circ + \frac{1}{2}\widehat {MNP}} \right) = 90^\circ - \frac{1}{2}\widehat {MNP}\) (1)

Vì DINH vuông tại H nên \(\widehat {HIN} + \widehat {HNI} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Suy ra \(\widehat {HIN} = 90^\circ - \widehat {HNI} = 90^\circ - \frac{1}{2}\widehat {MNP}\) (2)

Từ (1) và (2) suy ra \(\widehat {NIH} = \widehat {PIA}\).

Vậy ta chọn phương án C.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC vuông tại A. Các tia phân giác của các góc B và C cắt nhau tại I. Gọi H, J, K lần lượt là chân đường vuông góc kẻ từ I đến AB, AC, BC. Biết KI = 5 cm, BK = 10 cm, KC = 15 cm. Diện tích tam giác ABC bằng:

A. 75 cm²;

B. 100 cm²;

C. 150 cm²;

D. 300 cm².

Lời giải

Hướng dẫn giải

Đáp án đúng là:

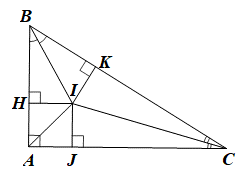
Media VietJack

Xét DBHI và DBKI có:

\(\widehat {BHI} = \widehat {BKI} = 90^\circ \),

BI là cạnh chung;

\(\widehat {HBI} = \widehat {KBI}\) (do BI là tia phân giác của góc ABC),

Do đó DBHI = DBKI (cạnh huyền – góc nhọn).

Suy ra BH = BK = 10 cm (hai cạnh tương ứng).

Chứng minh tương tự có DIJC = DIKC (cạnh huyền – góc nhọn).

Suy ra JC = KC = 15 cm.

Vì các tia phân giác của các góc B và C cắt nhau tại I nên I là giao điểm của ba đường phân giác của tam giác ABC.

Do đó AI là tia phân giác của góc A nên \(\widehat {HAI} = \widehat {JAI} = \frac{1}{2}.90^\circ = 45^\circ .\)

Tam giác AHI vuông tại H có \(\widehat {HAI} = 45^\circ \) nên là tam giác vuông cân tại H.

Do đó IH = AH.

Chứng minh tương tự ta cũng có tam giác AJI vuông cân tại J nên AJ = IJ.

Mà I là giao điểm của ba đường phân giác của tam giác ABC nên I cách đều ba cạnh của tam giác, hay IH = IK = IJ = 5 cm.

Suy ra AH = AJ = IH = IK = IJ = 5 cm.

Ta có AB = AH + BH = 5 + 10 = 15 (cm);

AC = AJ + JC = 5 + 15 = 20 (cm).

Diện tích tam giác ABC là:

\(\frac{1}{2}\).15.20 = 150 (cm²).

Vậy ta chọn phương án C.

Câu 2

Cho tam giác IHK có hai tia phân giác của góc H và góc K cắt nhau tại O. Khẳng định nào sau đây là đúng?

A. \(\widehat {I{\rm{O}}K} = 90^\circ - \frac{1}{2}\widehat {IHK}\);

B. \(\widehat {I{\rm{O}}K} = 90^\circ + \frac{1}{2}\widehat {IHK}\);

C. \(\widehat {I{\rm{O}}K} = 180^\circ - \frac{1}{2}\widehat {IHK}\);

D. \(\widehat {I{\rm{O}}K} = 180^\circ + \frac{1}{2}\widehat {IHK}\).

Lời giải

Hướng dẫn giải

Đáp án đúng là: B

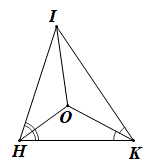
Media VietJack

Vì DIHK có hai tia phân giác của góc H và góc K cắt nhau tại O nên IO là tia phân giác của góc HIK.

Do đó \(\widehat {HIO} = \widehat {KIO} = \frac{1}{2}\widehat {HIK}\).

Vì KO là tia phân giác của góc HKI nên \(\widehat {HKO} = \widehat {IKO} = \frac{1}{2}\widehat {HKI}\).

Xét DOIK có \(\widehat {IKO} + \widehat {KIO} + \widehat {KOI} = 180^\circ \) (tổng ba góc trong một tam giác)

Nên \(\widehat {KOI} = 180^\circ - \left( {\widehat {IKO} + \widehat {KIO}} \right)\)

Suy ra \(\widehat {KOI} = 180^\circ - \frac{1}{2}\left( {\widehat {HKI} + \widehat {KIH}} \right)\)

Lại có \(\widehat {HKI} + \widehat {KIH} = 180^\circ - \widehat {IHK}\) (tổng ba góc trong tam giác HIK)

Nên \(\widehat {KOI} = 180^\circ - \frac{1}{2}\left( {180^\circ - \widehat {IHK}} \right) = 180^\circ - 90^\circ + \frac{1}{2}\widehat {IHK} = 90^\circ + \frac{1}{2}\widehat {IHK}\)

Vậy ta chọn phương án B.

Xem thêm các câu hỏi khác »

Hỏi bài tập