Cho ∆ABC vuông tại A. Trên cạnh AC lấy điểm M bất kì (M ≠ A, C). Qua M kẻ đường thẳng vuông góc với BC tại N. Từ C kẻ đường thẳng vuông góc với BM tại P. Gọi D là giao điểm của AB và CP. Khẳng định nào sau đây sai?
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D
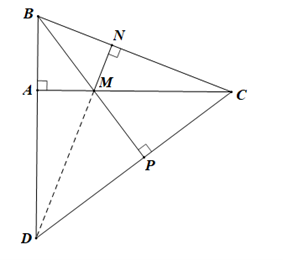
• Xét ∆DBC có CA, BP là hai đường cao cắt nhau tại M nên M là trực tâm của ∆DBC.
Do đó phương án A đúng.
• Vì M là trực tâm của ∆DBC nên DM ⊥ BC.
Do đó phương án B đúng.
• Ta có DM ⊥ BC (chứng minh trên).
Mà MN ⊥ BC (giả thiết).
Suy ra D, M, N thẳng hàng.
Do đó phương án C đúng.
• Ta có:
+) D ∈ MN (do D, M, N thẳng hàng);
+) D ∈ AB (giả thiết);
+) D ∈ CP (giả thiết).
Suy ra AB, MN, CP cùng đồng quy tại điểm D.
Do đó phương án D sai.
Vậy ta chọn phương án D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
B. 8 cm, 4 cm, 4 cm;
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
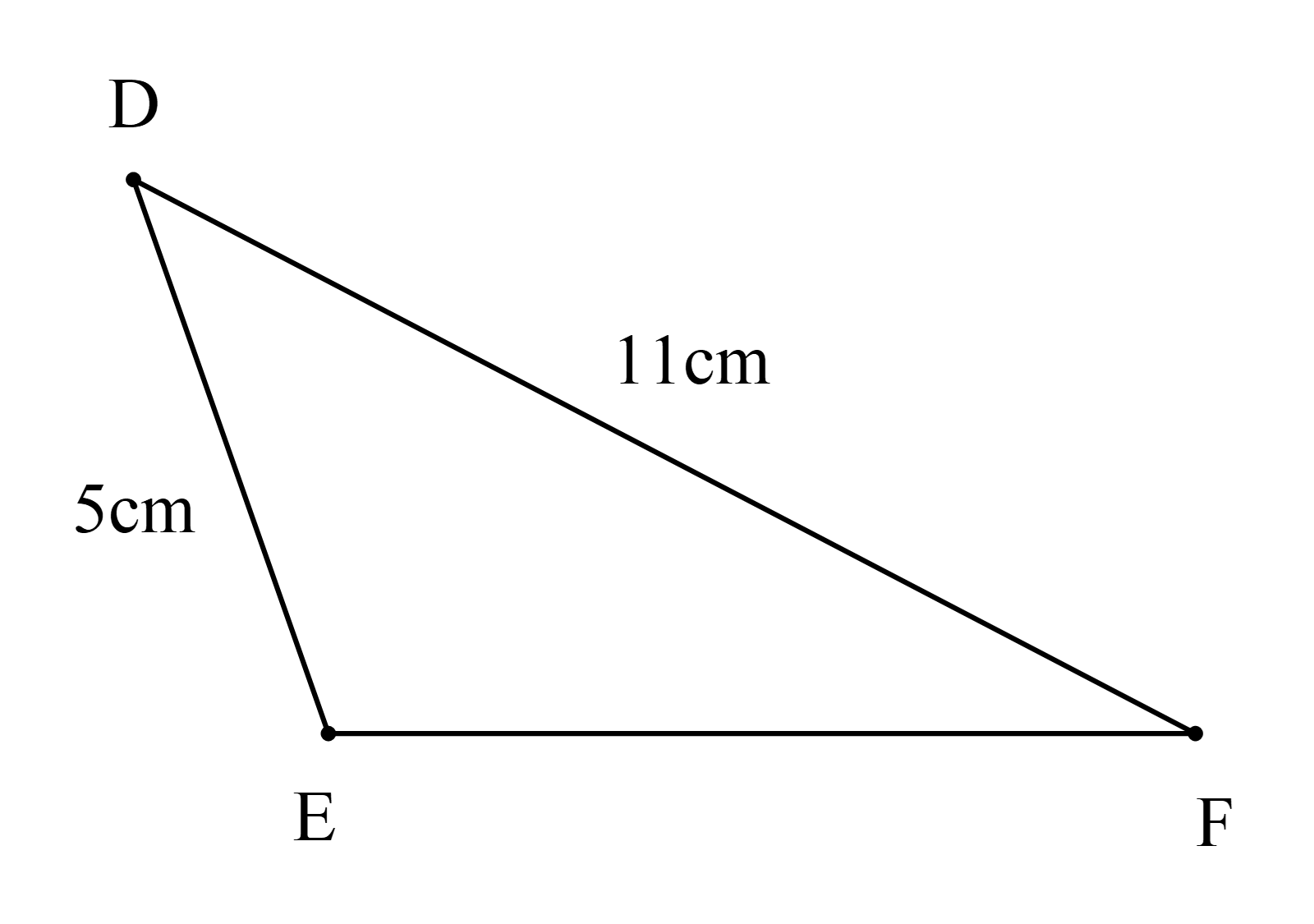
Ta có “Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng độ dài của hai cạnh còn lại”
Vì 6 cm < 2 cm + 3 cm = 5 cm, nên A sai;
8 cm = 4 cm + 4 cm, nên B sai;
8 cm = 5 cm + 3 cm, nên D sai;
7 cm – 5 cm < 9 cm < 7 cm + 5 cm, nên C đúng.
Vậy ta chọn phương án C.
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
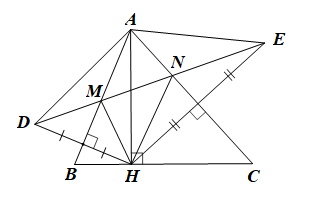
Xét DDHE có AB, AC là hai đường trung trực của tam giác cắt nhau tại A nên A cách đều ba đỉnh của tam giác
Do đó AD = AH = AE.
Tam giác ADE có AD = AE nên là tam giác cân tại A.
Suy ra \(\widehat {ADE} = \widehat {AED}\) (tính chất tam giác cân) (1)
Xét DADM và DAHM có
AM là cạnh chung,
DM = HM (do M thuộc trung trực của DH),
AD = AH (chứng minh trên).
Do đó DADM = DAHM (c.c.c).
Suy ra \(\widehat {ADM} = \widehat {AHM}\)(hai góc tương ứng) (2)
Xét DANH và DANE có
AN là cạnh chung,
NH = NE (do N thuộc trung trực của EH),
AH = AE (chứng minh trên)
Do đó DANH = DANE (c.c.c)
Suy ra \(\widehat {AHN} = \widehat {AEN}\)(hai góc tương ứng) (3)
Từ (1), (2) và (3) suy ra \(\widehat {AHN} = \widehat {AHM}\)
Do đó HA là tia phân giác của góc MHN.
Vậy ta chọn phương án C.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.