Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; –1) và B(3; 2). Tọa độ điểm M thuộc trục tung sao cho MA² + MB² nhỏ nhất là:

Hướng dẫn giải

Đáp án đúng là: B

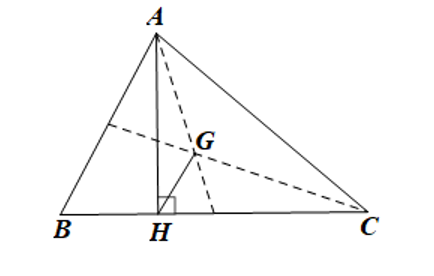
Gọi H có tọa độ là (a; b).

Với A(1; 4), B(2; 5), C(5; 2) và H(a; b) ta có:

• $\overrightarrow{AH}=\left(a-1;b-4\right)$;

• $\overrightarrow{BH}=\left(a-2;b-5\right)$ 

• $\overrightarrow{BC}=\left(3;-3\right)$.

+) Do AH vuông góc BC nên $\overrightarrow{AH}.\overrightarrow{BC}=0$ 

Û (a – 1).3 + (b – 4).(–3) = 0   

Û a – 1 – b + 4 = 0

Û a – b = – 3        (1)

$\overrightarrow{BH}$ cùng phương với $\overrightarrow{BC}$ nên ta có

(a – 2).(–3) – 3.(b – 5) = 0

Û – a + 2 – b + 5 = 0

Û a + b = 7          (2)

Từ (1) và (2) suy ra a = 2; b = 5 do đó H(2; 5).

+) G là trọng tâm tam giác ABC với A(1; 4), B(2; 5), C(5; 2) nên:

$x_G=\frac{1+2+5}{3}=\frac{8}{3};y_G=\frac{4+5+2}{3}=\frac{11}{3}$ 

Suy ra $G\left(\frac{8}{3};\frac{11}{3}\right)$.

Do đó $\overrightarrow{GH}=\left(-\frac{2}{3};\frac{4}{3}\right)$.

Độ dài GH là: $GH=\left|\overrightarrow{GH}\right|=\sqrt{{\left(-\frac{2}{3}\right)}^2+{\left(\frac{4}{3}\right)}^2}=\frac{2\sqrt{5}}{3}$.