Câu hỏi:
04/12/2022 347
Để đo khoảng cách giữa hai cột mốc M, N ngang qua hồ nước, người ta chọn một điểm G sao cho đường thẳng GM và GN đều ở bên ngoài hồ, rồi lấy hai điểm A, B sao cho G là trung điểm của AN và BM ( như hình vẽ). Chứng minh AB = MN.
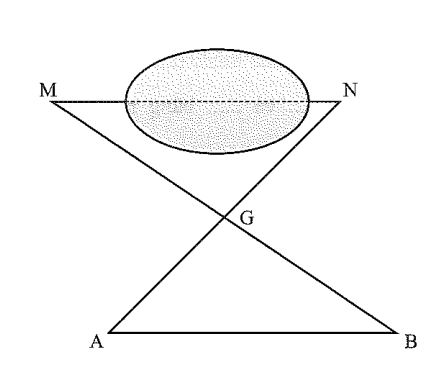
Để đo khoảng cách giữa hai cột mốc M, N ngang qua hồ nước, người ta chọn một điểm G sao cho đường thẳng GM và GN đều ở bên ngoài hồ, rồi lấy hai điểm A, B sao cho G là trung điểm của AN và BM ( như hình vẽ). Chứng minh AB = MN.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét ∆ GMN và ∆ GBA.
Theo giả thiết ta có: GM = GB; GN = GA.
Góc MGN = góc BGA ( hai góc đối đỉnh).
Vậy, hai tam giác GMN và GBA bằng nhau theo trường hợp c.g.c.
Suy ra AB = MN.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
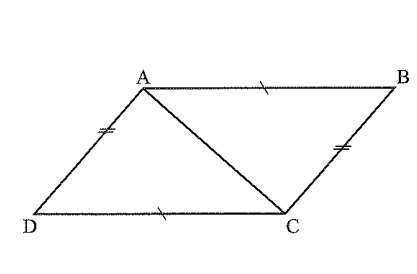
Xét ∆ ACD và ∆ CAB, theo giả thiết ta có:
AB = CD; AD = BC;
AC là cạnh chung.
Vậy ∆ ACD = ∆ CAB theo trường hợp c.c.c.
Suy ra góc ACD = góc CAB, mà hai góc ở vị trí so le trong nên AB // CD.
Lời giải
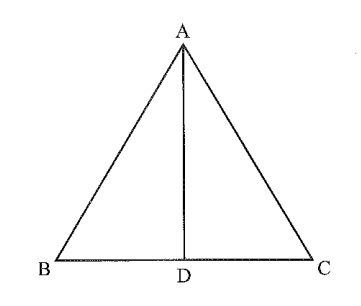
Xét ∆ ABD và ∆ ACD.
Theo giả thiết ta có: AB = AC; góc BAD = góc CAD;
AD là cạnh chung.
Vậy hai tam giác ABD và ACD bằng nhau theo trường hợp c.g.c.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 02
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận