Các nhà thiết kế đang xây dựng một phương án cho một khu công nghiệp. Trong khuôn viên này có bốn nhà máy tại bốn điểm A, B, C, D tạo thành một tứ giác. Người ta cần xây một nhà kho và đường đi để cung cấp nguyên liệu cho bốn nhà máy này. Hỏi nhà kho xây ở đâu để tổng khoảng cách tới bốn điểm A, B, C, D là bé nhất.
Các nhà thiết kế đang xây dựng một phương án cho một khu công nghiệp. Trong khuôn viên này có bốn nhà máy tại bốn điểm A, B, C, D tạo thành một tứ giác. Người ta cần xây một nhà kho và đường đi để cung cấp nguyên liệu cho bốn nhà máy này. Hỏi nhà kho xây ở đâu để tổng khoảng cách tới bốn điểm A, B, C, D là bé nhất.
Quảng cáo
Trả lời:
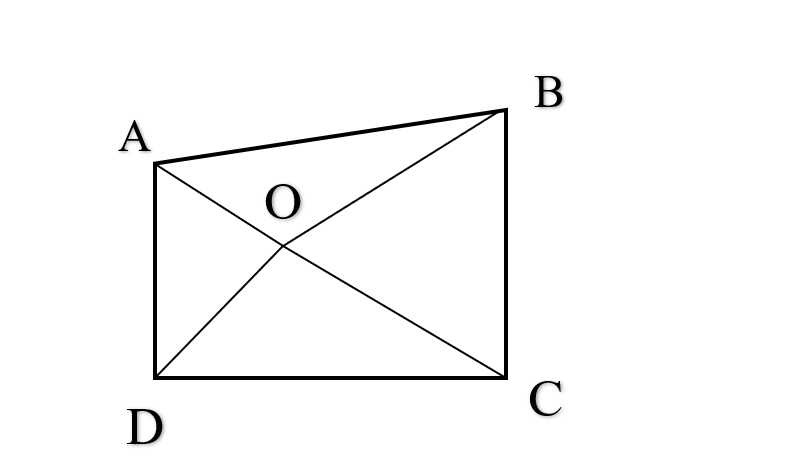
Gọi nơi xây nhà kho là điểm O. Ta có tổng khoảng cách tới 4 điểm A, B, C, D là:
OA + OB + OC + OD
Theo định lí về quan hệ giữa 3 cạnh của một tam giác:
OD + OB > BD.
OA + OC > AC.
OB + OD = BD và OA + OC = AC khi O là giao điểm của AC và BD.
Ta có OA + OB + OC + OD bé nhất bằng AC + BD khi O là giao điểm của AC và BD.
Vậy nhà kho xây ở điểm giao của AC và BD để tổng khoảng cách đến 4 nhà máy là bé nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
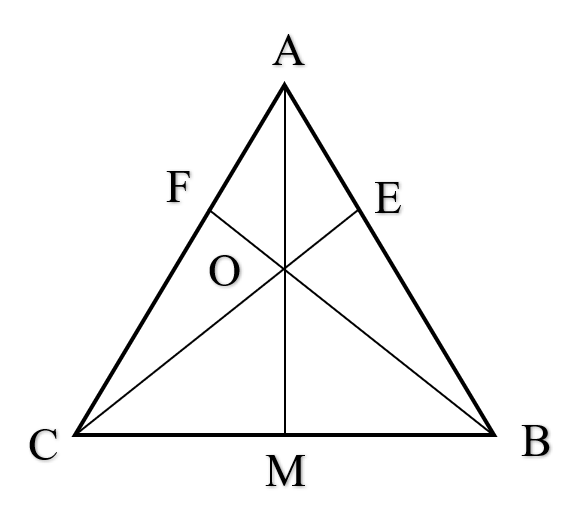
Kéo dài AO cắt BC tại M.
Xét tam giác ACE và tam giác ABF.
AC = AB ( do tam giác ABC cân tại A)
AE = AF (gt)
Góc A chung
Vậy tam giác ACE bằng tam giác ABF theo trường hợp c.g.c. Suy ra CE = BF.
Xét tam giác ECB và tam giác FBC
( do tam giác ABC cân tại A)
CE = BF
Cạnh chung BC
Vậy tam giác ECB bằng tam giác FBC theo trường hơpk c.g.c. Suy ra hay nên tam giác OBC cân tại O. Ta có OB = OC hay O nằm trên đường trung trực của BC (1).
AB = AC ( do tam giác ABC cân tại A) nên A nằm trên đường trung trực của BC. (2)
Từ (1) và (2) suy ra AO là đường trung trực của BC.
Lời giải
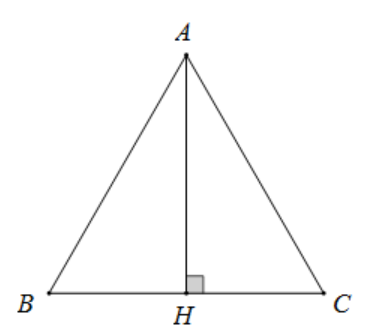
AH là đường cao của tam giác ABC nên .
AH là đường phân giác nên .
Xét tam giác AHB và tam giác AHC.
.
.
Cạnh chung AH.
Vậy tam giác AHB bằng tam giác AHC theo trường hợp g.c.g. Suy ra AB = AC hay tam giác ABC cân tại A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.