Trò chơi múc nước đổ vào thùng. Ba đội X, Y, Z cùng cắm trại tại ba địa điểm A, B, C. Nhiệm vụ của mỗi đội là múc nước từ một cái giếng để mang về đội của mình, đội nào múc được nhiều nước hơn sẽ thắng cuộc. Để cho công bằng, giếng nước phải xây tại một nơi mà khoảng cách tới ba địa điểm bằng nhau. Em hãy tìm chỗ đào giếng nước.
Trò chơi múc nước đổ vào thùng. Ba đội X, Y, Z cùng cắm trại tại ba địa điểm A, B, C. Nhiệm vụ của mỗi đội là múc nước từ một cái giếng để mang về đội của mình, đội nào múc được nhiều nước hơn sẽ thắng cuộc. Để cho công bằng, giếng nước phải xây tại một nơi mà khoảng cách tới ba địa điểm bằng nhau. Em hãy tìm chỗ đào giếng nước.
Quảng cáo
Trả lời:
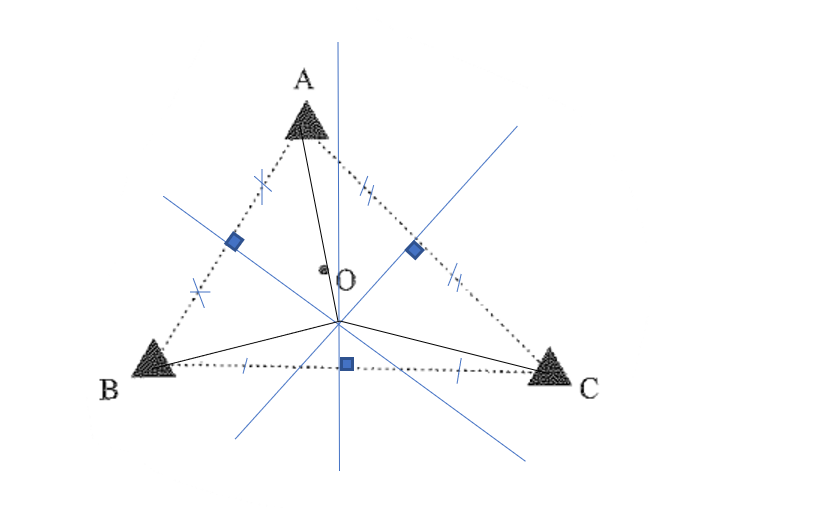
Ta kẻ đường trung trực của AB, AC. Điểm O là giao của hai đường trung trực của AB, AC. Suy ra O cũng là giao ba đường trung trực của tam giác ABC và điểm O cách đều 3 đỉnh của tam giác ABC hay OA = OB = OC. ( tính chất ba đường trung trực của tam giác).
Vậy điểm O chính là nơi cần tìm để đào giếng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
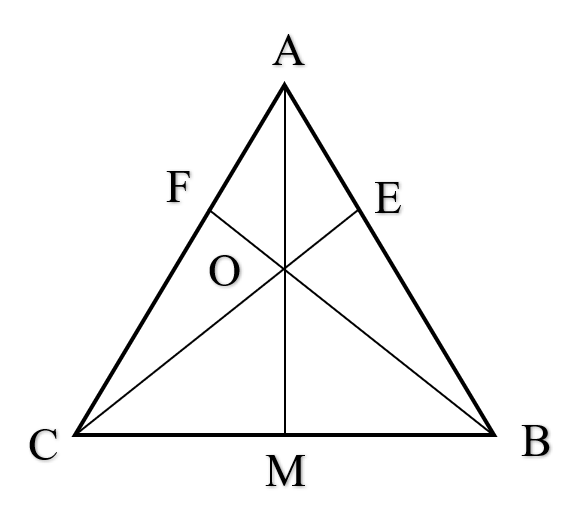
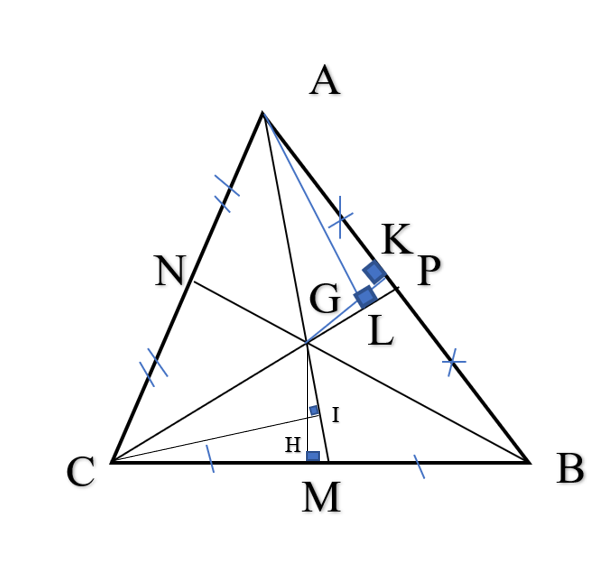
Kéo dài AO cắt BC tại M.
Xét tam giác ACE và tam giác ABF.
AC = AB ( do tam giác ABC cân tại A)
AE = AF (gt)
Góc A chung
Vậy tam giác ACE bằng tam giác ABF theo trường hợp c.g.c. Suy ra CE = BF.
Xét tam giác ECB và tam giác FBC
( do tam giác ABC cân tại A)
CE = BF
Cạnh chung BC
Vậy tam giác ECB bằng tam giác FBC theo trường hơpk c.g.c. Suy ra hay nên tam giác OBC cân tại O. Ta có OB = OC hay O nằm trên đường trung trực của BC (1).
AB = AC ( do tam giác ABC cân tại A) nên A nằm trên đường trung trực của BC. (2)
Từ (1) và (2) suy ra AO là đường trung trực của BC.
Lời giải
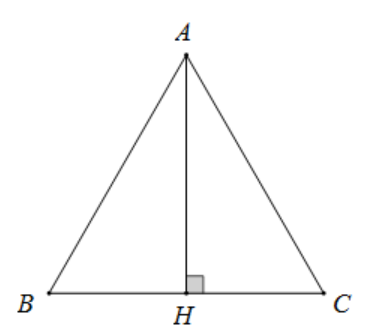
AH là đường cao của tam giác ABC nên .
AH là đường phân giác nên .
Xét tam giác AHB và tam giác AHC.
.
.
Cạnh chung AH.
Vậy tam giác AHB bằng tam giác AHC theo trường hợp g.c.g. Suy ra AB = AC hay tam giác ABC cân tại A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.