Câu hỏi:
22/12/2022 3,967
Cho đường tròn (C): (x – 2)2 + (y – 2)2 = 9. Phương trình tiếp tuyến của (C) đi qua điểm A(5; –1) là:
Cho đường tròn (C): (x – 2)2 + (y – 2)2 = 9. Phương trình tiếp tuyến của (C) đi qua điểm A(5; –1) là:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
Đường tròn (C) có tâm I(2; 2), bán kính R = 3.
Gọi d là tiếp tuyến cần tìm có vectơ pháp tuyến \(\vec n = \left( {A;B} \right)\).
Vì d đi qua điểm A(5; –1) nên phương trình d có dạng: A(x – 5) + B(y + 1) = 0.
⇔ Ax + By – 5A + B = 0.
Vì d là tiếp tuyến của (C) nên ta có d(I, d) = R.
\( \Leftrightarrow \frac{{\left| {A.2 + B.2 - 5A + B} \right|}}{{\sqrt {{A^2} + {B^2}} }} = 3\)
\( \Leftrightarrow \left| { - 3A + 3B} \right| = 3\sqrt {{A^2} + {B^2}} \)
⇔ 9A2 – 18AB + 9B2 = 9(A2 + B2)
⇔ AB = 0.
⇔ A = 0 hoặc B = 0.
Với A = 0, ta chọn B = 1.
Suy ra phương trình d: y + 1 = 0 ⇔ y = –1.
Với B = 0, ta chọn A = 1.
Suy ra phương trình d: x – 5 = 0 ⇔ x = 5.
Vậy có 2 tiếp tuyến thỏa mãn yêu cầu bài toán có phương trình là: y = –1 hoặc x = 5.
Do đó ta chọn phương án B.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có cách xếp 8 bạn học sinh vào hai dãy ghế có 8 ghế là hoán vị của 8 nên \(n\left( \Omega \right) = 8! = 40\,\,320\) cách xếp.
Gọi A là biến cố bất cứ hai học sinh nào ngồi đối diện nhau khác trường với nhau.
Ta có sơ đồ sau:
|
Dãy ghế thứ nhất |
1 |
2 |
3 |
4 |
|
Dãy ghế thứ hai |
5 |
6 |
7 |
8 |
Ở ghế 1: có 8 cách chọn học sinh ngồi vào ghế
Ở ghế 5: có 4 cách chọn học sinh ngồi vào ghế (khác trường với học sinh ghế 1).
Ở ghế 2: có 6 cách chọn học sinh ngồi vào ghế
Ở ghế 6: có 3 cách chọn học sinh ngồi vào ghế (khác trường với học sinh ghế 1).
Ở ghế 3: có 4 cách chọn học sinh ngồi vào ghế
Ở ghế 7: có 2 cách chọn học sinh ngồi vào ghế (khác trường với học sinh ghế 1).
Ở ghế 4: có 2 cách chọn học sinh ngồi vào ghế
Ở ghế 8: có 1 cách chọn học sinh ngồi vào ghế (khác trường với học sinh ghế 1).
Suy ra: n(A) = 8.4.6.3.4.2.2.1 = 9 216 cách xếp sao cho bất cứ hai học sinh nào ngồi cạnh nhau hoặc đối diện nhau khác trường với nhau.
Vì vậy \(P\left( A \right) = \frac{{9\,\,216}}{{40\,\,320}} = \frac{8}{{35}}\).
Lời giải
Đáp án đúng là: C
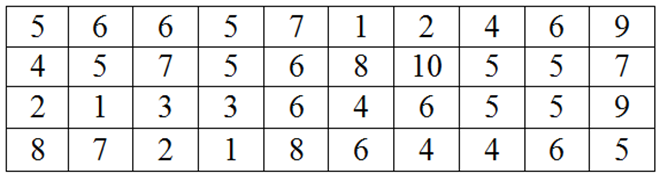
Ta có bảng tần số:
|
Điểm |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Tần số |
3 |
3 |
2 |
5 |
9 |
8 |
4 |
3 |
2 |
1 |
Khi đó điểm trung bình của lớp 10A là:
\(\overline x = \frac{{1.3 + 2.3 + 3.2 + 4.5 + 5.9 + 6.8 + 7.4 + 8.3 + 9.2 + 10.2}}{{40}} = 5,45\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
50 câu trắc nghiệm Thống kê cơ bản (phần 1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận