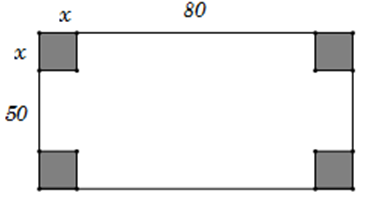
Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh , chiều cao là và thể tích là Tìm độ dài cạnh hình vuông sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.
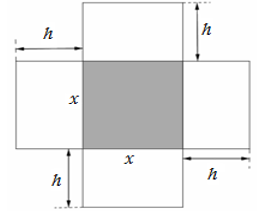
Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh , chiều cao là và thể tích là Tìm độ dài cạnh hình vuông sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.

A.
Quảng cáo
Trả lời:
Thể tích khối hộp
Để chiếc hộp làm ra ít tốn bìa các tông nhất khi và chỉ khi diện tích toàn phần của hộp là nhỏ nhất.
Diện tích toàn phần của hộp (không nắp)
Dấu xảy ra Chọn D.
Cách 2. Xét hàm với .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 320.000 đồng.
Lời giải
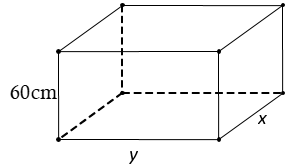
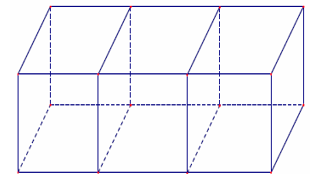
Gọi là chiều dài và chiều rộng của đáy bể.
Theo giả thiết, ta có:
Diện tích mặt đáy:
giá tiền đồng.Diện tích xung quanh:
giá tiền đồng.
Suy ra tổng chi phí
đồng. Chọn C.
Lời giải
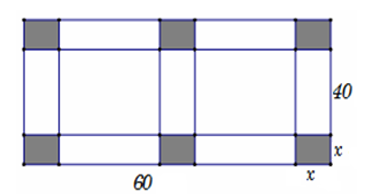
Hình hộp được tạo thành có kích thước: chiều dài , chiều rộng , chiều cao .
Suy ra thể tích thùng tạo thành .
Khảo sát trên , được
Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.