Cho các mệnh đề sau:
\(\left( I \right)\): Hàm số \(y = \sin x\) có chu kì là \(\frac{\pi }{2}\).
\(\left( {II} \right)\): Hàm số \(y = \tan x\) có tập giá trị là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
\(\left( {III} \right)\): Đồ thị hàm số \(y = \cos x\) đối xứng qua trục tung.
\(\left( {IV} \right)\): Hàm số \(y = \cot x\) đồng biến trên \(\left( { - \pi ;0} \right)\).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
Cho các mệnh đề sau:
\(\left( I \right)\): Hàm số \(y = \sin x\) có chu kì là \(\frac{\pi }{2}\).
\(\left( {II} \right)\): Hàm số \(y = \tan x\) có tập giá trị là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
\(\left( {III} \right)\): Đồ thị hàm số \(y = \cos x\) đối xứng qua trục tung.
\(\left( {IV} \right)\): Hàm số \(y = \cot x\) đồng biến trên \(\left( { - \pi ;0} \right)\).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
Câu hỏi trong đề: Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án !!
Quảng cáo
Trả lời:
Đáp án A
Phương pháp:
Nhận xét từng mệnh đề rồi kết luận.
Cách giải:
Hàm số \(y = \sin x\) có chu kỳ là \(2\pi \) nên I sai.
Hàm số \(y = \tan x\) xác định khi \(\cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)\) nên II đúng.
Ta có hàm số \(y = \cos x\) có \(y\left( x \right) = y\left( { - x} \right)\) nên đồ thị hàm số đối xứng với nhau qua trục tung nên III đúng.
Hàm số \(y = \cot x\) luôn nghịch biến trên R nên IV sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
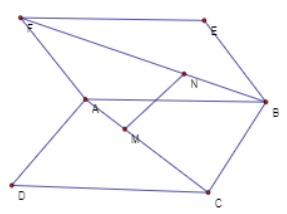
Câu 1
Lời giải
Đáp án A
Phương pháp:
Sử dụng tỉ số và định lí Ta-lét.
Cách giải:
Gọi N, P lần lượt thuộc SB, SC sao cho \(\frac{{SN}}{{SB}} = \frac{{SP}}{{SC}} = \frac{{SM}}{{SA}}\).
Khi đó thiết diện của mặt phẳng qua M song song với \(\left( {ABC} \right)\) là tam giác MNP.
Áp dụng định lí ta-lét trong tam giác SAB có: \(\frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{2}{3} = 4\)\(\left( {SM = 2MA;SA = 6} \right)\)
Tương tự ta có \(NP = MP = 4\,cm\).
Do đó tam giác MNP là tam giác đều cạnh 4cm.
\( \Rightarrow {S_{MNP}} = \frac{{\sqrt 3 }}{4}{.4^2} = 4\sqrt 3 c{m^2}\)
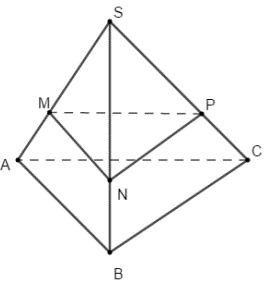
Câu 2
Lời giải
Đáp án A
Phương pháp:
Tìm điểm Q.
Sử dụng định lí Menelaus để tính tỉ số.
Cách giải:
Trong \(\left( {ABCD} \right)\) lấy \(PH||MN\left( {H \in CD} \right)\)
Trong \(\left( {SCD} \right)\) gọi \(Q = NH \cap SD\)
Áp dụng định lí Menelaus trong tam giác SCD với cát tuyến QNH ta có: \(\frac{{HD}}{{HC}}.\frac{{NC}}{{NS}}.\frac{{QS}}{{QD}} = 1\)
Mà N là trung điểm của SC \( \Rightarrow \frac{{NC}}{{NS}} = 1\).
Mặt khác áp dụng định lí Ta-lét trong tam giác DPH ta có \(\frac{{HD}}{{HC}} = \frac{{DP}}{{OP}} = 3\) (vì P là trung điểm của OB).
Do đó ta có \(\frac{{QS}}{{QD}} = \frac{1}{3} \Rightarrow \frac{{SQ}}{{SD}} = \frac{1}{4}\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.