Cho \[0 \le k \le n,k \in {\mathbb{N}^*},n \in {\mathbb{N}^*}.\] Số tổ hợp chập k của n phần tử được xác định bởi công thức nào sau đây?
Câu hỏi trong đề: Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án !!
Quảng cáo
Trả lời:
Đáp án D
Phương pháp:
Sử dụng công thức tính tổ hợp.
Cách giải:
\[C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}}\]
Chú ý: Phân biệt chỉnh hợp \[A_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\] và tổ hợp \[C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án B
Phương pháp:
Sử dụng tổ hợp và quy tắc nhân.
Cách giải:
Số cách chọn ra 2 viên bi xanh là: \[C_6^2.\]
Số cách chọn ra 2 viên bi đỏ là: \[C_4^1.\]
Số cách chọn từ hộp đó ra 3 viên bi gồm 2 viên bi xanh và 1 viên bi đỏ là \[C_6^2.C_4^1 = 60.\]
Lời giải
Phương pháp:
a) Xác định giao tuyến dựa vào yếu tố song song.
b) Chọn \[SC \subset \left( {SAC} \right),\] xác định giao tuyến \[\Delta = \left( {AMN} \right) \cap \left( {SAC} \right).\] Khi đó giao điểm của SC và \[\left( {AMN} \right)\] chính là giao điểm của SC và \[\Delta .\]
c) \[d||a \subset \left( P \right) \Rightarrow d||\left( P \right).\]
Cách giải:
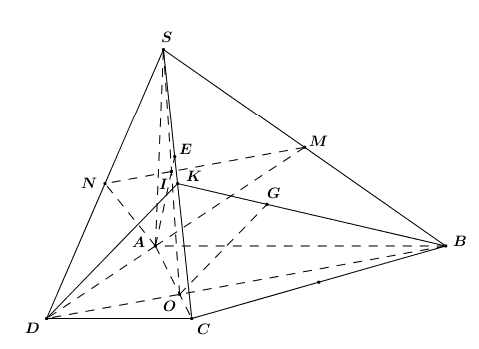
a) Xét \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\] có:
+ S là điểm chung thứ nhất.
+ \[\left\{ \begin{array}{l}\left( {SAB} \right) \supset AB\\\left( {SCD} \right) \supset CD\\AB||CD{\rm{ }}\left( {gt} \right)\end{array} \right. \Rightarrow \]Giao tuyến của \[\left( {SAB} \right),{\rm{ }}\left( {SCD} \right)\] là đường thẳng đi qua S và song song với AB, CD.
Trong \[\left( {SAB} \right)\] kẻ đường thẳng d đi qua S và \[d||AB||CD.\]
Vậy \[d = \left( {SAB} \right) \cap \left( {SCD} \right).\]
b) Chọn \[SC \subset \left( {SAC} \right),\] tìm giao tuyến của \[\left( {SAC} \right)\] và \[\left( {AMN} \right).\]
+ A là điểm chung thứ nhất.
+ Trong \[\left( {SBD} \right)\] gọi \[I = MN \cap SO\] ta có: \[I \in SO \subset \left( {SAC} \right) \Rightarrow I \in \left( {SAC} \right).\]
Trong \[\left( {SAC} \right)\] gọi \[E = AI \cap SC\] ta có:
\[\left\{ \begin{array}{l}E \in AI \subset \left( {AMN} \right) \Rightarrow E \in \left( {AMN} \right)\\E \in SC\end{array} \right. \Rightarrow E = SC \cap \left( {AMN} \right).\]
c) Gọi K là trung điểm của SC.
Vì G là trọng tâm tam giác SBC \[ \Rightarrow G \in BK\] và \[\frac{{BG}}{{BK}} = \frac{2}{3}\] (Tính chất trọng tâm).
Do \[AB||CD{\rm{ }}\left( {gt} \right),\] áp dụng định lí Ta-lét ta có: \[\frac{{BO}}{{OD}} = \frac{{AB}}{{CD}} = 2 \Rightarrow \frac{{BO}}{{BD}} = \frac{2}{3}.\]
\[ \Rightarrow \frac{{BG}}{{BK}} = \frac{{BO}}{{BD}} = \frac{2}{3} \Rightarrow OG||DK\] (Định lí Ta-lét đảo).
Mà \[DK \subset \left( {SCD} \right).\] Vậy \[OG||\left( {SCD} \right).\]
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Phương trình \[\cos x = \frac{1}{3}\] có bao nhiêu nghiệm trong khoảng \[\left( {0;2\pi } \right)?\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.