Trong đợt kết nạp Đoàn đầu năm của trường THPT X, kết quả có 15 học sinh khối 10 gồm 5 học sinh nam và 10 học sinh nữ, 35 học sinh khối 11 gồm 20 học sinh nam và 15 học sinh nữ được kết nạp. Chọn ngẫu nhiên từ các học sinh được kết nạp ra 3 học sinh đại diện lên nhận Huy hiệu Đoàn. Tính xác suất để trong 3 học sinh được chọn, có cả học sinh của hai khối, có cả học sinh nam và học sinh nữ, đồng thời số học sinh nam nhiều hơn số học sinh nữ.

Đáp án B

Phương pháp:

Sử dụng tổ hợp và quy tắc nhân.

Cách giải:

Số cách chọn ra 2 viên bi xanh là: \[C_6^2.\]

Số cách chọn ra 2 viên bi đỏ là: \[C_4^1.\]

Số cách chọn từ hộp đó ra 3 viên bi gồm 2 viên bi xanh và 1 viên bi đỏ là \[C_6^2.C_4^1 = 60.\]

Phương pháp:

a) Xác định giao tuyến dựa vào yếu tố song song.

b) Chọn \[SC \subset \left( {SAC} \right),\] xác định giao tuyến \[\Delta = \left( {AMN} \right) \cap \left( {SAC} \right).\] Khi đó giao điểm của SC và \[\left( {AMN} \right)\] chính là giao điểm của SC và \[\Delta .\]

c) \[d||a \subset \left( P \right) \Rightarrow d||\left( P \right).\]

Cách giải:

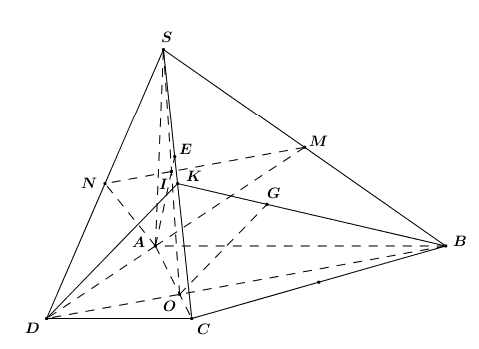
a) Xét \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\] có:

+ S là điểm chung thứ nhất.

+ \[\left\{ \begin{array}{l}\left( {SAB} \right) \supset AB\\\left( {SCD} \right) \supset CD\\AB||CD{\rm{ }}\left( {gt} \right)\end{array} \right. \Rightarrow \]Giao tuyến của \[\left( {SAB} \right),{\rm{ }}\left( {SCD} \right)\] là đường thẳng đi qua S và song song với AB, CD.

Trong \[\left( {SAB} \right)\] kẻ đường thẳng d đi qua S và \[d||AB||CD.\]

Vậy \[d = \left( {SAB} \right) \cap \left( {SCD} \right).\]

b) Chọn \[SC \subset \left( {SAC} \right),\] tìm giao tuyến của \[\left( {SAC} \right)\] và \[\left( {AMN} \right).\]

+ A là điểm chung thứ nhất.

+ Trong \[\left( {SBD} \right)\] gọi \[I = MN \cap SO\] ta có: \[I \in SO \subset \left( {SAC} \right) \Rightarrow I \in \left( {SAC} \right).\]

Trong \[\left( {SAC} \right)\] gọi \[E = AI \cap SC\] ta có:

\[\left\{ \begin{array}{l}E \in AI \subset \left( {AMN} \right) \Rightarrow E \in \left( {AMN} \right)\\E \in SC\end{array} \right. \Rightarrow E = SC \cap \left( {AMN} \right).\]

c) Gọi K là trung điểm của SC.

Vì G là trọng tâm tam giác SBC \[ \Rightarrow G \in BK\] và \[\frac{{BG}}{{BK}} = \frac{2}{3}\] (Tính chất trọng tâm).

Do \[AB||CD{\rm{ }}\left( {gt} \right),\] áp dụng định lí Ta-lét ta có: \[\frac{{BO}}{{OD}} = \frac{{AB}}{{CD}} = 2 \Rightarrow \frac{{BO}}{{BD}} = \frac{2}{3}.\]

\[ \Rightarrow \frac{{BG}}{{BK}} = \frac{{BO}}{{BD}} = \frac{2}{3} \Rightarrow OG||DK\] (Định lí Ta-lét đảo).

Mà \[DK \subset \left( {SCD} \right).\] Vậy \[OG||\left( {SCD} \right).\]