Sau vòng đấu bảng AFF CUP 2018, một tờ báo tại khu vực đã bình chọn đội hình tiêu biểu gồm 11 cầu thủ, trong đó, các đội tuyển Việt Nam, Malaysia, Thái Lan, Philippines mỗi đội có 2 cầu thủ, các đội tuyển Singapore, Myanmar, Indonesia mỗi đội có 1 cầu thủ. Tại buổi họp báo trước khi vào vòng đấu loại trực tiếp, ban tổ chức chọn ngẫu nhiên 5 cầu thủ trong đội hình tiêu biểu giao lưu cùng khán giả. Tính xác suất để 5 cầu thủ được chọn đến từ 5 đội tuyển khác nhau.

Đáp án B

Phương pháp:

Sử dụng tổ hợp và quy tắc nhân.

Cách giải:

Số cách chọn ra 2 viên bi xanh là: \[C_6^2.\]

Số cách chọn ra 2 viên bi đỏ là: \[C_4^1.\]

Số cách chọn từ hộp đó ra 3 viên bi gồm 2 viên bi xanh và 1 viên bi đỏ là \[C_6^2.C_4^1 = 60.\]

Phương pháp:

a) Xác định giao tuyến dựa vào yếu tố song song.

b) Chọn \[SC \subset \left( {SAC} \right),\] xác định giao tuyến \[\Delta = \left( {AMN} \right) \cap \left( {SAC} \right).\] Khi đó giao điểm của SC và \[\left( {AMN} \right)\] chính là giao điểm của SC và \[\Delta .\]

c) \[d||a \subset \left( P \right) \Rightarrow d||\left( P \right).\]

Cách giải:

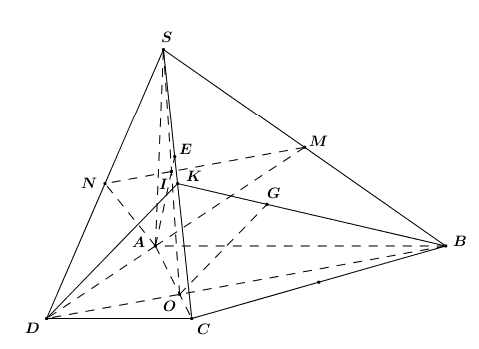
a) Xét \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\] có:

+ S là điểm chung thứ nhất.

+ \[\left\{ \begin{array}{l}\left( {SAB} \right) \supset AB\\\left( {SCD} \right) \supset CD\\AB||CD{\rm{ }}\left( {gt} \right)\end{array} \right. \Rightarrow \]Giao tuyến của \[\left( {SAB} \right),{\rm{ }}\left( {SCD} \right)\] là đường thẳng đi qua S và song song với AB, CD.

Trong \[\left( {SAB} \right)\] kẻ đường thẳng d đi qua S và \[d||AB||CD.\]

Vậy \[d = \left( {SAB} \right) \cap \left( {SCD} \right).\]

b) Chọn \[SC \subset \left( {SAC} \right),\] tìm giao tuyến của \[\left( {SAC} \right)\] và \[\left( {AMN} \right).\]

+ A là điểm chung thứ nhất.

+ Trong \[\left( {SBD} \right)\] gọi \[I = MN \cap SO\] ta có: \[I \in SO \subset \left( {SAC} \right) \Rightarrow I \in \left( {SAC} \right).\]

Trong \[\left( {SAC} \right)\] gọi \[E = AI \cap SC\] ta có:

\[\left\{ \begin{array}{l}E \in AI \subset \left( {AMN} \right) \Rightarrow E \in \left( {AMN} \right)\\E \in SC\end{array} \right. \Rightarrow E = SC \cap \left( {AMN} \right).\]

c) Gọi K là trung điểm của SC.

Vì G là trọng tâm tam giác SBC \[ \Rightarrow G \in BK\] và \[\frac{{BG}}{{BK}} = \frac{2}{3}\] (Tính chất trọng tâm).

Do \[AB||CD{\rm{ }}\left( {gt} \right),\] áp dụng định lí Ta-lét ta có: \[\frac{{BO}}{{OD}} = \frac{{AB}}{{CD}} = 2 \Rightarrow \frac{{BO}}{{BD}} = \frac{2}{3}.\]

\[ \Rightarrow \frac{{BG}}{{BK}} = \frac{{BO}}{{BD}} = \frac{2}{3} \Rightarrow OG||DK\] (Định lí Ta-lét đảo).

Mà \[DK \subset \left( {SCD} \right).\] Vậy \[OG||\left( {SCD} \right).\]