Câu hỏi:

07/02/2023 7,985

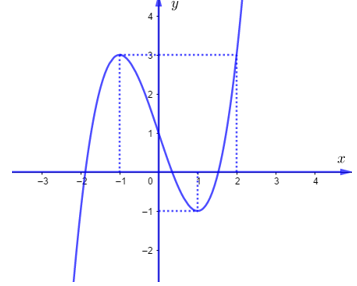
Cho hàm số y=f(x) xác định, liên tục trên R và có đúng hai điểm cực trị x=-1,x=1, có đồ thị như hình vẽ sau: Hỏi hàm số y=f( $x^{2}$ -2x+1)+2020 có bao nhiêu điểm cực tiểu?

A. 4

B. 3

C. 2

D. 1

Xem lời giải

Câu hỏi trong đề: Bộ 20 đề thi giữa học kì 1 Toán 12 năm 2022-2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn C

Do hàm số y=f(x) có đúng hai điểm cực trị x=-1 , x=1 nên phương trình f'(x)=0 có hai nghiệm bội lẻ phân biệt x=-1, x=1. Dấu của

f'(x)

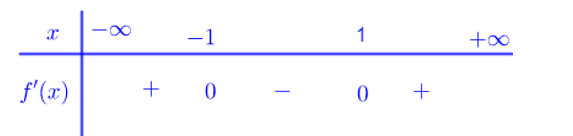
Cho hàm số y=f(x) xác định, liên tục trên R và có đúng hai điểm cực trị x=-1,x=1, có đồ thị như hình vẽ sau: Hỏi hàm số y=f(x^2-2x+1)+2020 (ảnh 1)

Ta có Cho hàm số y=f(x) xác định, liên tục trên R và có đúng hai điểm cực trị x=-1,x=1, có đồ thị như hình vẽ sau: Hỏi hàm số y=f(x^2-2x+1)+2020 (ảnh 2)

Cho hàm số y=f(x) xác định, liên tục trên R và có đúng hai điểm cực trị x=-1,x=1, có đồ thị như hình vẽ sau: Hỏi hàm số y=f(x^2-2x+1)+2020 (ảnh 3)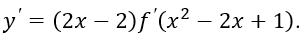

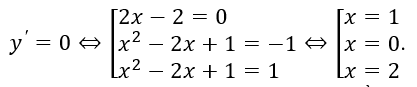
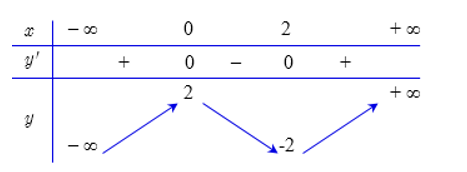
Ta có: 3 nghiệm 0, 1, 2 của y'=0 đều là nghiệm bội lẻ nên y' đổi dấu khi qua các điểm này. Mặt khác với x>2 thì 2x-2>0 và

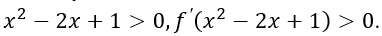
Cho hàm số y=f(x) xác định, liên tục trên R và có đúng hai điểm cực trị x=-1,x=1, có đồ thị như hình vẽ sau: Hỏi hàm số y=f(x^2-2x+1)+2020 (ảnh 4)

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số $y = a x^{3} + b x^{2} + c x + d (a \neq 0)$ có bảng biến thiên như sau:

Tính $S = a + b .$

A. $S = - 1.$

B. $S = - 2.$

C. $S = 1.$

D. $S = 0.$

Lời giải

Chọn B

Ta có: $y^{'} = 3 a x^{2} + 2 b x + c$ .

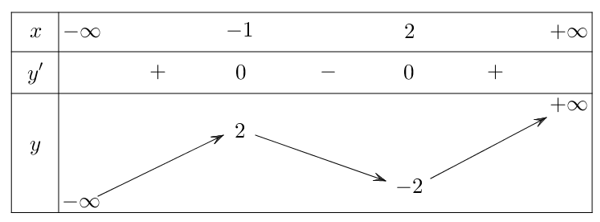
Từ bảng biến thiên, ta thấy: hàm số đạt cực trị tại $x = 0, x = 2$ nên $y^{'} (0) = y^{'} (2) = 0$ .

Đồ thị đi qua các điểm $(0; 2); (2; - 2)$ .

Ta có hệ $\{\begin{cases} y^{'} (0) = 0 \\ y^{'} (2) = 0 \\ y (0) = 2 \\ y (2) = - 2 \end{cases} \Leftrightarrow \{\begin{cases} c = 0 \\ 12 a + 4 b + c = 0 \\ d = 2 \\ 8 a + 4 b + 2 c + d = - 2 \end{cases} \Leftrightarrow \{\begin{cases} a = 1 \\ b = - 3 \\ c = 0 \\ d = 2 \end{cases}$ . Suy ra $S = a + b = - 2.$

Câu 2

Tìm tất cả giá trị của tham số m để hàm số $f (x) = x^{3} + 3 x^{2} + m^{2} - 5$ có giá trị lớn nhất trên đoạn $[- 1; 2]$ là 19.

A. m=2 và m=3

B. m =1 và m=-2

C. m =2 và m=-2

D. m=1 và m=3

Lời giải

Tìm tất cả giá trị của tham số m để hàm số f(x)= x^3+3x^2+m^2-5 có giá trị lớn nhất trên đoạn [ -1,2] là 19. (ảnh 1)

Câu 3

Các khoảng đồng biến của hàm số $y = x^{3} + 3 x$ là

A. $(0; 2)$

B. R

C. $(- \infty; 1)$ và $(2; + \infty)$

D. $(0; + \infty)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hàm số $y = f (x)$ liên tục trên R, có đạo hàm $f^{'} (x) = {(x - 2)}^{4} + 1$ . Khẳng định nào sau đây đúng?

A. Hàm số

y = f (x)

đồng biến trên khoảng

(- \infty; 2)

và nghịch biến trên khoảng

(2; + \infty)

B. Hàm số

y = f (x)

đồng biến trên khoảng

(2; + \infty)

và nghịch biến trên khoảng

(- \infty; 2)

C. Hàm số

y = f (x)

đồng biến trên khoảng

(- \infty; + \infty)

D. Hàm số

y = f (x)

nghịch biến trên khoảng

(- \infty; + \infty)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Hình lăng trụ tam giác có bao nhiêu cạnh?

A. 9

B. 12

C. 6

D. 10

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số y=f(x) có đồ thị như hình vẽ bên dưới:

Hàm số có bao nhiêu điểm cực tiểu trên khoảng (a,b)?

A. 2

B. 7

C. 4

D. 3

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Giáo dục công dân

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học