Câu hỏi:
22/02/2023 1,060
Cho hàm số \(y = \frac{{2x - 1}}{{x + 1}}\) có đồ thị \(\left( H \right)\). Có bao nhiêu điểm trên đồ thị \(\left( H \right)\) thỏa mãn cách đều 2 tiệm cận của đồ thị hàm số?
Cho hàm số \(y = \frac{{2x - 1}}{{x + 1}}\) có đồ thị \(\left( H \right)\). Có bao nhiêu điểm trên đồ thị \(\left( H \right)\) thỏa mãn cách đều 2 tiệm cận của đồ thị hàm số?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Phương pháp:
Đồ thị hàm số \(y = \frac{{ax + b}}{{cx + d}},\,\left( {ad - bc \ne 0,\,c \ne 0} \right)\) có TCN là\(y = \frac{a}{c}\) và TCĐ: \(x = - \frac{d}{c}\)
Cách giải:
Đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 1}}\) có TCN là \(y = 2\) và TCĐ: \(x = 1\)
Giả sử \(H\left( {{x_0};{y_0}} \right) \in \left( H \right) \Rightarrow {y_0} = \frac{{2{x_0} - 1}}{{{x_0} + 1}} \Rightarrow H\left( {{x_0};\frac{{2{x_0} - 1}}{{{x_0} + 1}}} \right)\)
Khoảng cách từ \(H\left( {{x_0};\frac{{2{x_0} - 1}}{{{x_0} + 1}}} \right)\) đến đường thẳng \(y = 2\) là: \(\left| {\frac{{2{x_0} - 1}}{{{x_0} + 1}} - 2} \right| = \left| {\frac{{ - 3}}{{{x_0} + 1}}} \right| = \frac{3}{{\left| {{x_0} + 1} \right|}}\)
Khoảng cách từ \(H\left( {{x_0};\frac{{2{x_0} - 1}}{{{x_0} + 1}}} \right)\) đến đường thẳng \(x = - 1\) là \(\left| {{x_0} + 1} \right|\)
Theo đề bài, ta có: \(\frac{3}{{\left| {{x_0} + 1} \right|}} = \left| {{x_0} + 1} \right| \Leftrightarrow {\left| {{x_0} + 1} \right|^2} = 3 \Leftrightarrow \left| {{x_0} + 1} \right| = \sqrt 3 \Leftrightarrow {x_0} = - 1 \pm \sqrt 3 \)
\( \Rightarrow \) Có 2 điểm H thỏa mãn.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án A
Phương pháp:
\({\log _a}f\left( x \right)\) xác định \( \Leftrightarrow f\left( x \right) > 0\)
Cách giải:
ĐKXĐ: \({x^2} - 2x - 3 > 0 \Leftrightarrow x \in \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
Vậy TXĐ: \(\left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
Lời giải
Đáp án A
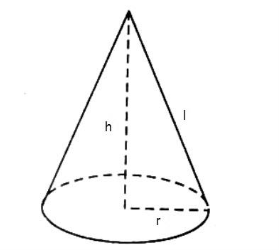
Phương pháp:
Thể tích khối nón: \(V = \frac{1}{3}\pi {r^2}h\)
Cách giải:
\(V = \frac{1}{3}\pi {r^2}h \Rightarrow 4\pi = \frac{1}{3}\pi {r^2}.3 \Rightarrow {r^2} = 4 \Rightarrow r = 2\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận