Câu hỏi:
22/02/2023 1,136
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác đều SAB và nằm trong mặt phẳng vuông góc với đáy. Tính bán kính của mặt cầu ngoại tiếp hình chóp.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác đều SAB và nằm trong mặt phẳng vuông góc với đáy. Tính bán kính của mặt cầu ngoại tiếp hình chóp.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án A
Phương pháp:
Xác định tâm mặt cầu ngoại tiếp hình chóp
Tính bán kính mặt cầu.
Cách giải:
Gọi M là trung điểm của AB; G là trọng tâm tam giác SAB; O là tâm của
hình vuông ABCD
Do tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy nên \(SM \bot \left( {ABCD} \right)\)
\( \Rightarrow SMO = {90^0}\). Dựng hình chữ nhật GMOI. Khi đó:
\(OI//GM \Rightarrow OI \bot \left( {ABCD} \right) \Rightarrow IA = IB = IC = ID\,\,\left( 1 \right)\)
Mặt khác \(GI//MO\), mà \(MO \bot AB,\,\,MO \bot SM \Rightarrow MO \bot \left( {SAB} \right)\)
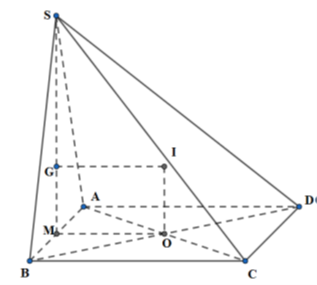
\( \Rightarrow GI \bot \left( {SAB} \right) \Rightarrow IA = IS = IB\,\,\,\left( 2 \right)\)
Từ (1), (2) \( \Rightarrow \) I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD
Ta có: G là trọng tâm tam giác đều SAB
\( \Rightarrow GM = \frac{1}{3}.SM = \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6} \Rightarrow OI = \frac{{a\sqrt 3 }}{6}\)
ABCD là hình vuông cạnh a \( \Rightarrow OB = \frac{{BD}}{2} = \frac{{a\sqrt 2 }}{2}\)
GMOI là hình chữ nhật
\( \Rightarrow IB = \sqrt {O{I^2} + O{B^2}} = \sqrt {\frac{1}{{12}}{a^2} + \frac{1}{2}{a^2}} = \sqrt {\frac{7}{{12}}} a = \frac{{a\sqrt {21} }}{6}\)
Vậy, bán kính của mặt cầu ngoại tiếp hình chóp là: \(\frac{{a\sqrt {21} }}{6}\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án A
Phương pháp:
\({\log _a}f\left( x \right)\) xác định \( \Leftrightarrow f\left( x \right) > 0\)
Cách giải:
ĐKXĐ: \({x^2} - 2x - 3 > 0 \Leftrightarrow x \in \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
Vậy TXĐ: \(\left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
Lời giải
Đáp án A
Phương pháp:
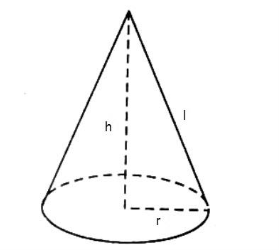
Thể tích khối nón: \(V = \frac{1}{3}\pi {r^2}h\)
Cách giải:
\(V = \frac{1}{3}\pi {r^2}h \Rightarrow 4\pi = \frac{1}{3}\pi {r^2}.3 \Rightarrow {r^2} = 4 \Rightarrow r = 2\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận