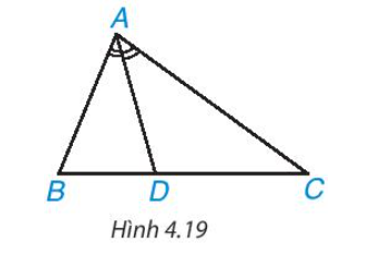
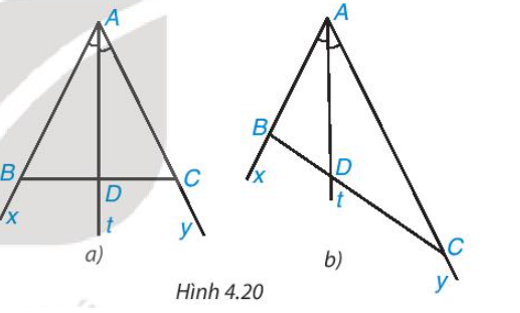
Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D.
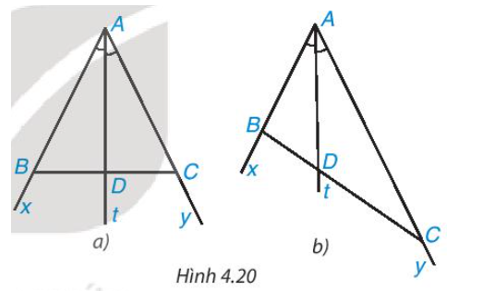 Khi lấy B và C sao cho AB = AC (H.4.20a), hãy so sánh tỉ số và .
Khi lấy B và C sao cho AB = AC (H.4.20a), hãy so sánh tỉ số và .
Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D.

Quảng cáo
Trả lời:
Theo đề bài, At là tia phân giác của góc xAy hay AD là tia phân giác của góc BAC.
Tam giác ABC cân tại A (vì AB = AC) có AD là tia phân giác của góc BAC nên AD cũng là đường trung tuyến của tam giác ABC.
Suy ra D là trung điểm của cạnh BC hay DB = DC nên .
Vì AB = AC nên .
Vậy khi lấy B và C sao cho AB = AC thì .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
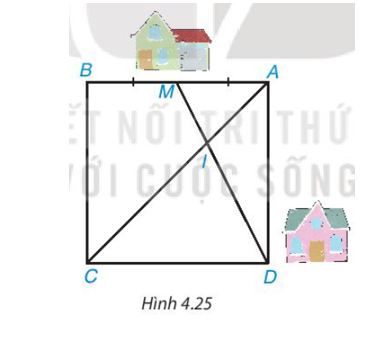
Theo đề bài, ABCD là hình vuông nên AB = AD và AC là tia phân giác của .
Vì M là trung điểm của AB nên hay .
Vì AC là tia phân giác của hay AI là tia phân giác của , áp dụng tính chất đường phân giác trong tam giác ADM, ta có:
suy ra ID = 2IM.
Giả sử vận tốc đi bộ của bạn Mai và bạn Dung đều bằng nhau.
Theo đề bài, I là địa điểm gặp nhau nên bạn Mai đi theo quãng đường MI, bạn Dung đi theo quãng đường DI.
Vì quãng đường bạn Dung đi gấp 2 lần quãng đường bạn Mai đi và vận tốc đi bộ của hai bạn đều bằng nhau (giả sử) nên thời gian bạn Dung đi gấp 2 lần thời gian bạn Mai đi thì hai bạn mới gặp nhau tại địa điểm I.
Bạn Dung gặp bạn Mai lúc 7h30 nên thời gian bạn Mai đi trên quãng đường MI là:
7h30 – 7h = 30 phút.
Khi đó, thời gian bạn Dung đi là 1h. Do đó, bạn Dung xuất phát từ lúc:
7h30 – 1h = 6h30.
Vậy bạn Dung xuất phát lúc 6h30 để gặp bạn Mai lúc 7h30 tại điểm I.
Lời giải
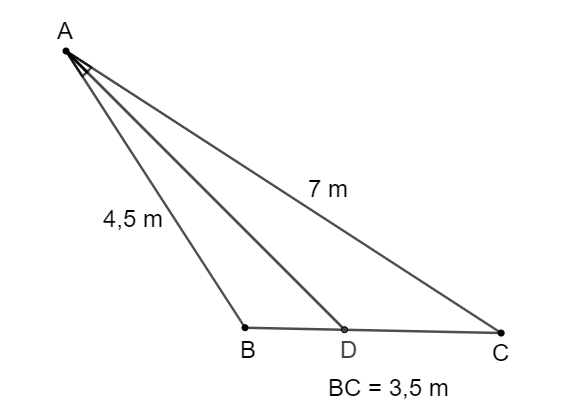
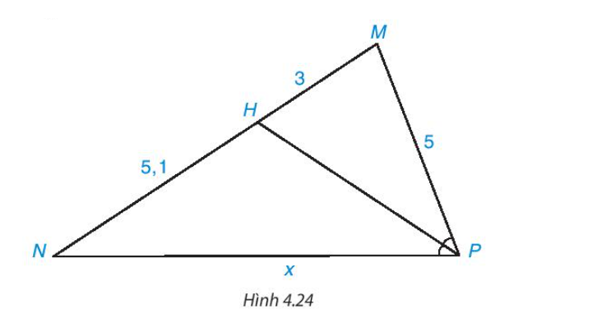
Theo đề bài, đường phân giác trong của góc A cắt BC tại D nên AD là tia phân giác của .
Áp dụng tính chất đường phân giác của tam giác, ta có:
hay nên .
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
.
Suy ra (m)
Vậy DC ≈ 2,1 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.