Câu hỏi:

13/07/2024 1,056

Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K lần lượt là trung điểm của GB, GC. Chứng minh tứ giác EDKI là hình bình hành.

Xem lời giải

Câu hỏi trong đề: Giải SGK Toán 8 KNTT Bài tập cuối chương 4 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

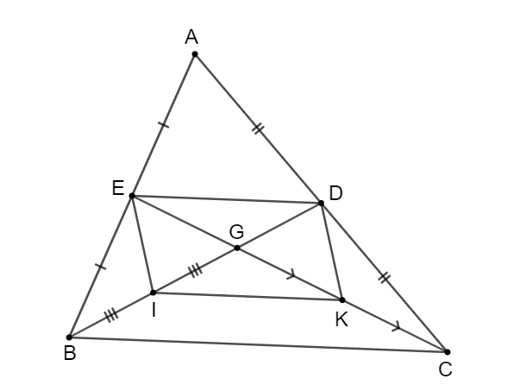
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K lần lượt (ảnh 1)

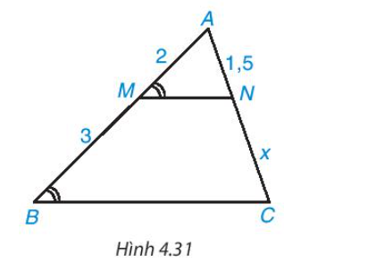
Vì BD và CE là đường trung tuyến nên E, D lần lượt là trung điểm của AB, AC.

Suy ra DE là đường trung bình của tam giác ABC.

Khi đó, DE // BC và $D E = \frac{1}{2} B C$ (1)

Vì I, K lần lượt là trung điểm của GB, GC nên IK là đường trung bình của tam giác GBC suy ra IK // BC và $I K = \frac{1}{2} B C$ (2)

Từ (1) và (2) suy ra DE // IK và $D E = I K = \frac{1}{2} B C$ .

Tứ giác EDKI có DE // IK và DE = IK nên tứ giác EDKI là hình bình hành (đpcm).

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC.

a) Chứng minh rằng AE = DF.

Xem đáp án

Lời giải

Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC. (ảnh 1)

a) Theo đề bài, tam giác ABC vuông tại A nên $\hat{B A C} = 90 °$ hay AB ⊥ AC.

Vì D, E lần lượt là trung điểm của AB, BC nên DE là đường trung bình của tam giác ABC suy ra DE // AC.

Mà AB ⊥ AC nên AB ⊥ DE hay $\hat{A D E} = 90 °$ .

Tương tự, ta chứng minh được: EF ⊥ AC hay $\hat{A F E} = 90 °$ .

Ta có: $\hat{B A C} + \hat{A D E} + \hat{A F E} + \hat{D E F} = 360 °$

90 ° + 90 ° + 90 ° + \hat{D E F} = 360 °

270 ° + \hat{D E F} = 360 °

Suy ra $\hat{D E F} = 360 ° - 270 ° = 90 °$ .

Tứ giác ADEF có $\hat{B A C} = 90 °; \hat{A D E} = 90 °; \hat{A F E} = 90 °; \hat{D E F} = 90 °$ .

Do đó tứ giác ADEF là hình chữ nhật.

Suy ra hai đường chéo AE và DF bằng nhau.

Vậy AE = DF (đpcm).

Câu 2

Bác Mến muốn tính khoảng cách giữa hai vị trí P, Q ở hai bên bờ ao cá. Để làm điều đó, bác Mến chọn ba vị trí A, B, C, thực hiện đo đạc và vẽ mô phỏng như Hình 4.32. Em hãy giúp bác Mến tính khoảng cách giữa hai điểm P và Q.

Xem đáp án

Lời giải

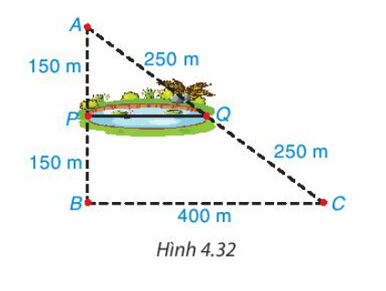
Trong Hình 4.32 có AP = BP = 150 m; AQ = CQ = 250 m.

Suy ra PQ là đường trung bình của tam giác ABC.

Do đó $P Q = \frac{1}{2} B C = \frac{1}{2} . 400 = 200$ (m)

Vậy khoảng cách giữa hai điểm P và Q là 200 m.

Câu 3

Cho tam giác ABC cân tại A có AB = 15 cm, BC = 10 cm, đường phân giác trong của góc B cắt AC tại D. Khi đó, đoạn thẳng AD có độ dài là

A. 3 cm.

B. 6 cm.

C. 9 cm.

D. 12 cm.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho tam giác ABC có chu vi là 32 cm. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chu vi của tam giác MNP là

A. 8 cm.

B. 64 cm.

C. 30 cm.

D. 16 cm.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho tam giác ABC. Gọi H, K lần lượt là trung điểm của AC, BC. Biết HK = 3,5 cm. Độ dài AB bằng

A. 3,5 cm.

B. 7 cm.

C. 10 cm.

D. 15 cm.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Độ dài x trong Hình 4.31 bằng

A. 2,75

B. 2.

C. 2,25.

D. 3,75.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

b) Gọi I là trung điểm của DE. Chứng minh rằng ba điểm B, I, F thẳng hàng.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K lần lượt là trung điểm của GB, GC. Chứng minh tứ giác EDKI là hình bình hành.

Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC. a) Chứng minh rằng AE = DF.

Bác Mến muốn tính khoảng cách giữa hai vị trí P, Q ở hai bên bờ ao cá. Để làm điều đó, bác Mến chọn ba vị trí A, B, C, thực hiện đo đạc và vẽ mô phỏng như Hình 4.32. Em hãy giúp bác Mến tính khoảng cách giữa hai điểm P và Q.

Cho tam giác ABC cân tại A có AB = 15 cm, BC = 10 cm, đường phân giác trong của góc B cắt AC tại D. Khi đó, đoạn thẳng AD có độ dài là A. 3 cm. B. 6 cm. C. 9 cm. D. 12 cm.

Cho tam giác ABC có chu vi là 32 cm. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chu vi của tam giác MNP là A. 8 cm. B. 64 cm. C. 30 cm. D. 16 cm.

Cho tam giác ABC. Gọi H, K lần lượt là trung điểm của AC, BC. Biết HK = 3,5 cm. Độ dài AB bằng A. 3,5 cm. B. 7 cm. C. 10 cm. D. 15 cm.

Độ dài x trong Hình 4.31 bằng A. 2,75 B. 2. C. 2,25. D. 3,75.

b) Gọi I là trung điểm của DE. Chứng minh rằng ba điểm B, I, F thẳng hàng.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC.

a) Chứng minh rằng AE = DF.

Cho tam giác ABC cân tại A có AB = 15 cm, BC = 10 cm, đường phân giác trong của góc B cắt AC tại D. Khi đó, đoạn thẳng AD có độ dài là

A. 3 cm.

B. 6 cm.

C. 9 cm.

D. 12 cm.

Cho tam giác ABC có chu vi là 32 cm. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chu vi của tam giác MNP là

A. 8 cm.

B. 64 cm.

C. 30 cm.

D. 16 cm.

Cho tam giác ABC. Gọi H, K lần lượt là trung điểm của AC, BC. Biết HK = 3,5 cm. Độ dài AB bằng

A. 3,5 cm.

B. 7 cm.

C. 10 cm.

D. 15 cm.

Độ dài x trong Hình 4.31 bằng

A. 2,75

B. 2.

C. 2,25.

D. 3,75.