Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân MNPQ (Hình 13) với hai đáy MN = 6 cm, PQ = 10 cm và độ dài hai đường chéo MP = NQ = cm. Tính độ dài đường cao và cạnh bên của hình thang.
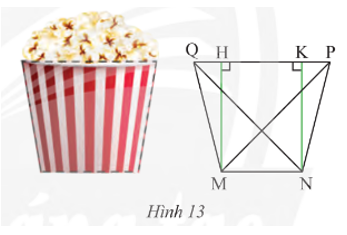
Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân MNPQ (Hình 13) với hai đáy MN = 6 cm, PQ = 10 cm và độ dài hai đường chéo MP = NQ = cm. Tính độ dài đường cao và cạnh bên của hình thang.

Quảng cáo
Trả lời:
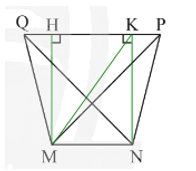
• MNPQ là hình thang cân nên MN // QP; MQ = NP; (tính chất hình thang cân).
• Ta có: MN // QP (chứng minh trên) và NK ⊥ QP (giả thiết)
Suy ra NK ⊥ MN hay .
Xét DMHK và DKNM có:
;
MK là cạnh huyền chung;
(hai góc so le trong của QP // MN).
Do đó DMHK = DKNM (cạnh huyền – góc nhọn)
Suy ra HK = NM = 6 cm (hai cạnh tương ứng).
• Xét DMHQ và DNKP có:
;
MQ = NP (chứng minh trên);
(chứng minh trên).
Do đó DMHQ = DNKP (cạnh huyền – góc nhọn).
Suy ra QH = PK (hai cạnh tương ứng).
Mà QH + HK + PK = QP
Hay 2QH = QP – HK
Khi đó QH = PK =
Nên HP = HK + KP = 6 + 2 = 8 (cm).
• Áp dụng định lí Pythagore vào DMHP vuông tại H, ta có:
MP2 = MH2 + HP2
Suy ra MH2 = MP2 – HP2 =
Do đó MH = 8 cm.
Áp dụng định lí Pythagore vào DMHQ vuông tại H, ta có:
MQ2 = MH2 + HQ2 = 82 + 22 = 64 + 4 = 68
Suy ra (cm).
Vậy hình thang cân MNPQ có độ dài đường cao là MH = NK = 8 cm; độ dài cạnh bên là MQ = NP = cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
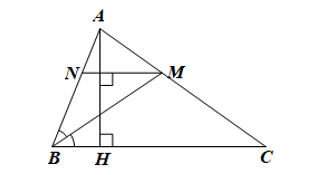
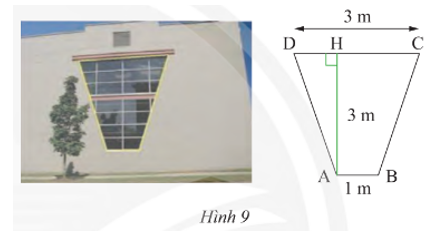
a) Ta có AH ⊥ BC, AH ⊥ NM nên BC // NM
Tứ giác BCMN có BC // NM nên là hình thang.
Lời giải
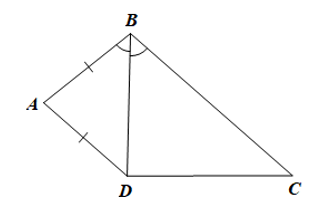
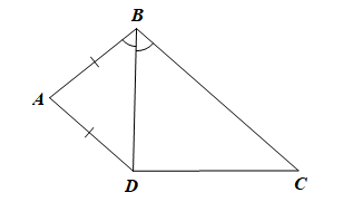
Xét DABD có AB = AD nên là tam giác cân tại A
Suy ra (tính chất tam giác cân)
Vì BD là tia phân giác của góc B nên (tính chất tia phân giác của một góc)
Suy ra
Mà hai góc này ở vị trí so le trong nên AD // BC.
Xét tứ giác ABCD có AD // BC nên là hình thang.
Vậy ABCD là hình thang.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.