Câu hỏi:

12/07/2024 2,534

b) Kẻ đường cao AH của tam giác ABC. Chứng minh rằng tứ giác ADEH là hình thang vuông.

Xem lời giải

Câu hỏi trong đề: Giải SGK Toán 8 CTST Bài 3. Hình thang – Hình thang cân có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

b) Do DABD = DEBD (câu a) nên $\hat{B A D} = \hat{B E D} = 90 °$ (hai góc tương ứng).

Do đó DE ⊥ BC

Mà AH ⊥ BC (giả thiết) nên DE // AH.

Tứ giác ADEH có DE // AH nên là hình thang

Lại có $\hat{A H E} = 90 °$ nên ADEH là hình thang vuông.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH và cắt AB tại N. Chứng minh rằng:

a) Tứ giác BCMN là hình thang;

b) BN = MN.

Xem đáp án

Lời giải

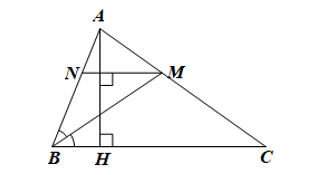
Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH và cắt AB tại N. Chứng minh rằng: (ảnh 1)

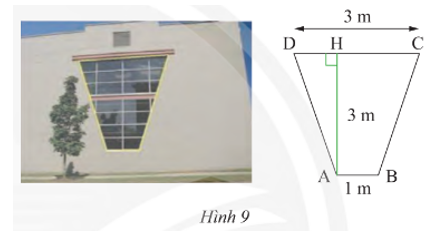
a) Ta có AH ⊥ BC, AH ⊥ NM nên BC // NM

Tứ giác BCMN có BC // NM nên là hình thang.

Câu 2

Cho tứ giác ABCD có AB = AD, BD là tia phân giác của góc B. Chứng minh rằng ABCD là hình thang.

Xem đáp án

Lời giải

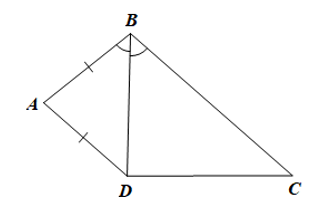
Cho tứ giác ABCD có AB = AD, BD là tia phân giác của góc B. Chứng minh rằng ABCD là hình thang. (ảnh 2)

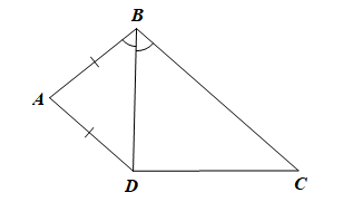
Xét DABD có AB = AD nên là tam giác cân tại A

Suy ra $\hat{A B D} = \hat{A D B}$ (tính chất tam giác cân)

Vì BD là tia phân giác của góc B nên $\hat{A B D} = \hat{C B D}$ (tính chất tia phân giác của một góc)

Suy ra $\hat{C B D} = \hat{A D B} (= \hat{A B D})$

Mà hai góc này ở vị trí so le trong nên AD // BC.

Xét tứ giác ABCD có AD // BC nên là hình thang.

Vậy ABCD là hình thang.

Câu 3

Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại D. Trên BC lấy điểm E sao cho BE = BA.

a) Chứng minh rằng DABD = DEBD.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tìm x và y ở các hình sau.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một khung cửa sổ hình thang cân có chiều cao 3 m, hai đáy là 3 m và 1 m (Hình 9). Tìm độ dài hai cạnh bên và hai đường chéo.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình thang cân ABCD có AB // CD. Qua giao điểm E của AC và BD, ta vẽ đường thẳng song song với AB và cắt AD, BC lần lượt tại F và G (Hình 16). Chứng minh rằng EG là tia phân giác của góc CEB.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Tìm các góc chưa biết của hình thang MNPQ có hai đáy là MN và QP trong mỗi trường hợp sau và nêu nhận xét của em.

a) $\hat{Q} = 90 °$ và $\hat{N} = 125 °$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

b) Kẻ đường cao AH của tam giác ABC. Chứng minh rằng tứ giác ADEH là hình thang vuông.

Bình luận

Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH và cắt AB tại N. Chứng minh rằng: a) Tứ giác BCMN là hình thang; b) BN = MN.

Cho tứ giác ABCD có AB = AD, BD là tia phân giác của góc B. Chứng minh rằng ABCD là hình thang.

Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại D. Trên BC lấy điểm E sao cho BE = BA. a) Chứng minh rằng DABD = DEBD.

Tìm x và y ở các hình sau.

Một khung cửa sổ hình thang cân có chiều cao 3 m, hai đáy là 3 m và 1 m (Hình 9). Tìm độ dài hai cạnh bên và hai đường chéo.

Cho hình thang cân ABCD có AB // CD. Qua giao điểm E của AC và BD, ta vẽ đường thẳng song song với AB và cắt AD, BC lần lượt tại F và G (Hình 16). Chứng minh rằng EG là tia phân giác của góc CEB.

Tìm các góc chưa biết của hình thang MNPQ có hai đáy là MN và QP trong mỗi trường hợp sau và nêu nhận xét của em. a) Q^=90° và N^=125°.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH và cắt AB tại N. Chứng minh rằng:

a) Tứ giác BCMN là hình thang;

b) BN = MN.

Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại D. Trên BC lấy điểm E sao cho BE = BA.

a) Chứng minh rằng DABD = DEBD.

Tìm các góc chưa biết của hình thang MNPQ có hai đáy là MN và QP trong mỗi trường hợp sau và nêu nhận xét của em.

a) $\hat{Q} = 90 °$ và $\hat{N} = 125 °$ .