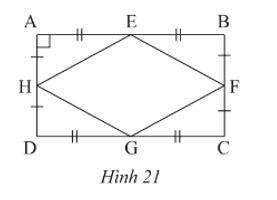
Cho hình bình hành ABCD, kẻ AH vuông góc với BD tại H và CK vuông góc với BD tại K (Hình 20).
a) Chứng minh tứ giác AHCK là hình bình hành.
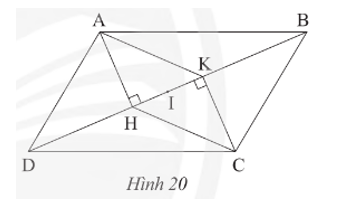
Cho hình bình hành ABCD, kẻ AH vuông góc với BD tại H và CK vuông góc với BD tại K (Hình 20).
a) Chứng minh tứ giác AHCK là hình bình hành.

Quảng cáo
Trả lời:
a) Do ABCD là hình bình hành nên AD // BC và AD = BC.
Do AD // BC nên (so le trong)
Xét DADH và DCBK có:
;
AD = BC (chứng minh trên);
(do ).
Do đó DADH = DCBK (cạnh huyền – góc nhọn).
Suy ra AH = CK (hai cạnh tương ứng).
Ta có AH ⊥ DB và CK ⊥ DB nên AH // CK.
Tứ giác AHCK có AH // CK và AH = CK nên AHCK là hình bình hành (dấu hiệu nhận biết).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có D đối xứng với A qua BC nên M là trung điểm của AD và AD ⊥ BC.
Tứ giác ABDC có hai đường chéo AD và BD cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
Lại có hai đường chéo AD ⊥ BC nên hình bình hành ABDC là hình thoi.
Lời giải
a)
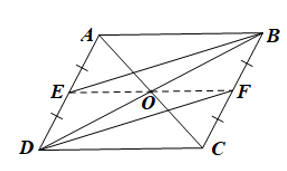
ABCD là hình bình hành nên AD = BC và AD // BC.
Mà E là trung điểm của AD nên AE = ED;
F là trung điểm của BC nên BF = FC.
Suy ra DE = BF.
Xét tứ giác EBFD có DE // BF (do AD // BC) và DE = BF nên là hình bình hành (dấu hiệu nhận biết).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.