Cho tứ giác MNPQ gọi R, S, T, V theo tứ tự là trung điểm của MN, NP, PQ, QM.
a) Chứng minh rằng RSTV là hình bình hành.
b) Nếu MP vuông góc với NQ thì RQTV là hình gì?
Cho tứ giác MNPQ gọi R, S, T, V theo tứ tự là trung điểm của MN, NP, PQ, QM.
a) Chứng minh rằng RSTV là hình bình hành.
b) Nếu MP vuông góc với NQ thì RQTV là hình gì?
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
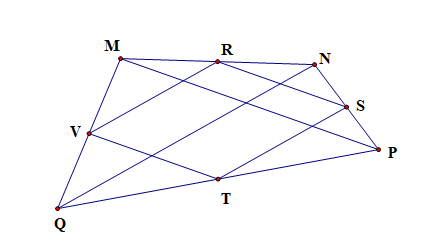
• Xét ΔMNQ có: R, V lần lượt là trung điểm của MN, MQ
Do đó RV là đường trung bình của ΔMNQ
Suy ra RV // NQ và \(RV = \frac{1}{2}NQ\) (1)
• Xét ΔNPQ có: T, S lần lượt là trung điểm của QP, NP
Do đó TS là đường trung bình của ΔNPQ
Suy ra TS // NQ và \(T{\rm{S}} = \frac{1}{2}NQ\) (2)
Từ (1) và (2) suy ra RV // TS và RV = TS
Do đó RSTV là hình bình hành.
b) Xét ΔMNP có: R, S lần lượt là trung điểm MN, NP
Suy ra RS là đường trung bình của ΔMNP
Do đó RS // MP
Mà MP ⊥ NQ, nên RS ⊥ NQ (quan hệ từ vuông góc đến song song)
Lại có ST // NQ
Suy ra RS ⊥ ST hay \(\widehat {RST} = 90^\circ \).
Xét hình bình hành RSTV có \(\widehat {RST} = 90^\circ \)
Suy ra RSTV là hình chữ nhật
Vậy nếu MP vuông góc với NQ thì RQTV là hình chữ nhật.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
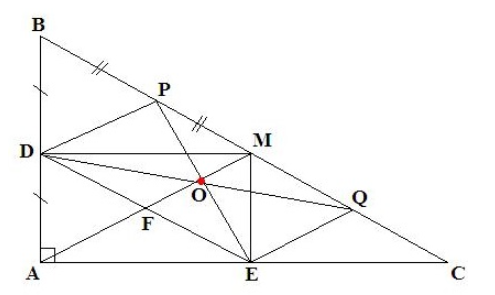
a) Ta có D, E là hình chiếu của M trên AB, AC
Nên DM ⊥ AB và ME ⊥ AC, hay \(\widehat {A{\rm{D}}M} = \widehat {A{\rm{E}}M} = 90^\circ \)
Xét tứ giác ADME có \(\widehat {DA{\rm{E}}} = \widehat {A{\rm{D}}M} = \widehat {A{\rm{E}}M} = 90^\circ \)
Suy ra ADME là hình chữ nhật.
b) Xét ΔABC vuông tại A có M là trung điểm BC
Suy ra \(AM = \frac{1}{2}BC\)
Vì ADME là hình chữ nhật có AM, DE là hai đường chéo, suy ra AM = DE
Mà \(AM = \frac{1}{2}BC\)
Do đó \(DE = \frac{1}{2}BC\).
c) Ta có AD ⊥ AC và ME ⊥ AC, suy ra AD // ME
Mà M là trung điểm của BC
Suy ra E là trung điểm của AC
Xét tam giác AMC có E, Q lần lượt là trung điểm của AC, MC
Suy ra QE là đường trung bình
Do đó QE // AM, \(QE = \frac{1}{2}AM\) (1)
Ta có DM ⊥ AB và AB ⊥ AC
Suy ra DM // AC
Mà M là trung điểm của BC
Suy ra D là trung điểm của AB
Xét ΔBAM có D, P lần lượt là trung điểm của AB và BM
Suy ra DP là đường trung bình của ΔBAM
Do đó DP // AM và \(DP = \frac{1}{2}AM\) (2)
Từ (1) và (2) suy ra DP // EQ, DP = EQ
Do đó DPQE là hình bình hành.
Gọi O là tâm đối xứng của DPQE (là giao điểm 2 đường chéo)
Ta có P, Q lần lượt là trung điểm của BM, MC và M là trung điểm BC
Suy ra M là trung điểm PQ
Xét hình bình hành DPQE có AM // DP và M là trung điểm PQ
Suy ra AM là đường trung bình của DPQE
Do đó AM đi qua trung điểm DE, gọi điểm đó là F
Từ đó AM là trục đối xứng của DPQE tức là đi qua O
Vậy tâm đối xứng của hình bình hành DPQE nằm trên đoạn AM.
d) Để hình bình hành DPQE là hình chữ nhật thì \(\widehat {APQ} = \widehat {PQE} = \widehat {QE{\rm{D}}} = \widehat {E{\rm{D}}P} = 90^\circ \)
Ta xét ΔBAM nếu DP ⊥ BM thì AM ⊥ BM
Xét ΔABC có AM vừa là đường trung tuyến vừa là đường cao
Suy ra ΔABC vuông cân tại A
Vậy để hình bình hành DPQE là hình chữ nhật thì tam giác vuông ΔABC cần thêm điều kiện cân tại A.
Lời giải
Lời giải
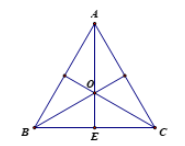
a) Ta có
\(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.c{\rm{os}}\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = AB.AC.c{\rm{os}}\widehat {BAC} = a.a.c{\rm{os60}}^\circ = \frac{{{a^2}}}{2}\).
b) Ta có
\(\overrightarrow {AB} .\overrightarrow {BC} = - \overrightarrow {BA} .\overrightarrow {BC} = - BA.BC.cos\left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = - BA.BC.co{\rm{s60}}^\circ {\rm{ = }}\frac{{ - {a^2}}}{2}\).
c) Gọi E là trung điểm của BC.
Suy ra \(\overrightarrow {OB} + \overrightarrow {OC} = 2\overrightarrow {OE} \).
Ta có \(\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right)\left( {\overrightarrow {AB} - \overrightarrow {AC} } \right)\)
\( = 2\overrightarrow {OE} .\overrightarrow {CB} \)
\( = 2{\rm{O}}E.CB.co{\rm{s}}\left( {\overrightarrow {OE} ,\overrightarrow {CB} } \right)\)
\( = 2{\rm{O}}E.CB.\cos 90^\circ = 0\).
d) Ta có \(\overrightarrow {AC} .\overrightarrow {BC} = \overrightarrow {AC} .\overrightarrow {BC} = AC.BC.cos\left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = AC.BC.co{\rm{s60}}^\circ {\rm{ = }}\frac{{{a^2}}}{2}\)
Ta có \(\left( {\overrightarrow {AB} + 2\overrightarrow {AC} } \right)\left( {\overrightarrow {AB} - 3\overrightarrow {BC} } \right)\)
\( = {\overrightarrow {AB} ^2} - 3\overrightarrow {AB} .\overrightarrow {BC} + 2\overrightarrow {AB} .\overrightarrow {AC} - 6\overrightarrow {AC} .\overrightarrow {BC} \)
\( = {a^2} + \frac{{3{{\rm{a}}^2}}}{2} + {a^2} - 3{{\rm{a}}^2} = \frac{{{a^2}}}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.