Cho \(\left( {{\rm{x}} + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = 1\). Tính x + y.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
Ta có \(\left( {{\rm{x}} + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = 1\)
\( \Leftrightarrow \left( {\sqrt {{x^2} + 1} - x} \right)\left( {{\rm{x}} + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = \sqrt {{x^2} + 1} - x\)
\( \Leftrightarrow \left( {{x^2} + 1 - {x^2}} \right)\left( {y + \sqrt {{y^2} + 1} } \right) = \sqrt {{x^2} + 1} - x\)
\( \Leftrightarrow y + \sqrt {{y^2} + 1} = \sqrt {{x^2} + 1} - x\) (1)
Ta có \(\left( {{\rm{x}} + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = 1\)
\( \Leftrightarrow \left( {\sqrt {{x^2} + 1} - x} \right)\left( {y + \sqrt {{y^2} + 1} } \right)\left( {\sqrt {{y^2} + 1} - y} \right) = \sqrt {{y^2} + 1} - y\)
\( \Leftrightarrow \left( {\sqrt {{x^2} + 1} - x} \right)\left( {{y^2} + 1 - {y^2}} \right) = \sqrt {{y^2} + 1} - y\)
\( \Leftrightarrow \sqrt {{x^2} + 1} - x = \sqrt {{y^2} + 1} - y\)
\( \Leftrightarrow \sqrt {{y^2} + 1} - y = \sqrt {{x^2} + 1} - x\) (2)
Trừ vế theo vế của (1) cho (2) ta được
2y = 0
Û y = 0
Thay y = 0 vào (1) ta được \(1 = \sqrt {{x^2} + 1} - x\)
\( \Leftrightarrow \sqrt {{x^2} + 1} = x + 1\)
\( \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\{x^2} + 1 = {\left( {x + 1} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\{x^2} + 1 = {x^2} + 2x + 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\2x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\x = 0\end{array} \right. \Leftrightarrow x = 0\)
Do đó x + y = 0 + 0 = 0.
Vậy x + y = 0.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
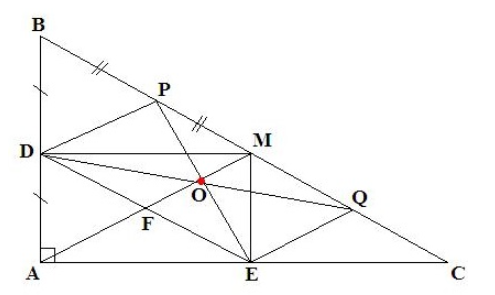
a) Ta có D, E là hình chiếu của M trên AB, AC
Nên DM ⊥ AB và ME ⊥ AC, hay \(\widehat {A{\rm{D}}M} = \widehat {A{\rm{E}}M} = 90^\circ \)
Xét tứ giác ADME có \(\widehat {DA{\rm{E}}} = \widehat {A{\rm{D}}M} = \widehat {A{\rm{E}}M} = 90^\circ \)
Suy ra ADME là hình chữ nhật.
b) Xét ΔABC vuông tại A có M là trung điểm BC
Suy ra \(AM = \frac{1}{2}BC\)
Vì ADME là hình chữ nhật có AM, DE là hai đường chéo, suy ra AM = DE
Mà \(AM = \frac{1}{2}BC\)
Do đó \(DE = \frac{1}{2}BC\).
c) Ta có AD ⊥ AC và ME ⊥ AC, suy ra AD // ME
Mà M là trung điểm của BC
Suy ra E là trung điểm của AC
Xét tam giác AMC có E, Q lần lượt là trung điểm của AC, MC
Suy ra QE là đường trung bình
Do đó QE // AM, \(QE = \frac{1}{2}AM\) (1)
Ta có DM ⊥ AB và AB ⊥ AC
Suy ra DM // AC
Mà M là trung điểm của BC
Suy ra D là trung điểm của AB
Xét ΔBAM có D, P lần lượt là trung điểm của AB và BM
Suy ra DP là đường trung bình của ΔBAM
Do đó DP // AM và \(DP = \frac{1}{2}AM\) (2)
Từ (1) và (2) suy ra DP // EQ, DP = EQ
Do đó DPQE là hình bình hành.
Gọi O là tâm đối xứng của DPQE (là giao điểm 2 đường chéo)
Ta có P, Q lần lượt là trung điểm của BM, MC và M là trung điểm BC
Suy ra M là trung điểm PQ
Xét hình bình hành DPQE có AM // DP và M là trung điểm PQ
Suy ra AM là đường trung bình của DPQE
Do đó AM đi qua trung điểm DE, gọi điểm đó là F
Từ đó AM là trục đối xứng của DPQE tức là đi qua O
Vậy tâm đối xứng của hình bình hành DPQE nằm trên đoạn AM.
d) Để hình bình hành DPQE là hình chữ nhật thì \(\widehat {APQ} = \widehat {PQE} = \widehat {QE{\rm{D}}} = \widehat {E{\rm{D}}P} = 90^\circ \)
Ta xét ΔBAM nếu DP ⊥ BM thì AM ⊥ BM
Xét ΔABC có AM vừa là đường trung tuyến vừa là đường cao
Suy ra ΔABC vuông cân tại A
Vậy để hình bình hành DPQE là hình chữ nhật thì tam giác vuông ΔABC cần thêm điều kiện cân tại A.
Lời giải
Lời giải
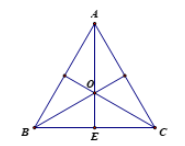
a) Ta có
\(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.c{\rm{os}}\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = AB.AC.c{\rm{os}}\widehat {BAC} = a.a.c{\rm{os60}}^\circ = \frac{{{a^2}}}{2}\).
b) Ta có
\(\overrightarrow {AB} .\overrightarrow {BC} = - \overrightarrow {BA} .\overrightarrow {BC} = - BA.BC.cos\left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = - BA.BC.co{\rm{s60}}^\circ {\rm{ = }}\frac{{ - {a^2}}}{2}\).
c) Gọi E là trung điểm của BC.
Suy ra \(\overrightarrow {OB} + \overrightarrow {OC} = 2\overrightarrow {OE} \).
Ta có \(\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right)\left( {\overrightarrow {AB} - \overrightarrow {AC} } \right)\)
\( = 2\overrightarrow {OE} .\overrightarrow {CB} \)
\( = 2{\rm{O}}E.CB.co{\rm{s}}\left( {\overrightarrow {OE} ,\overrightarrow {CB} } \right)\)
\( = 2{\rm{O}}E.CB.\cos 90^\circ = 0\).
d) Ta có \(\overrightarrow {AC} .\overrightarrow {BC} = \overrightarrow {AC} .\overrightarrow {BC} = AC.BC.cos\left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = AC.BC.co{\rm{s60}}^\circ {\rm{ = }}\frac{{{a^2}}}{2}\)
Ta có \(\left( {\overrightarrow {AB} + 2\overrightarrow {AC} } \right)\left( {\overrightarrow {AB} - 3\overrightarrow {BC} } \right)\)
\( = {\overrightarrow {AB} ^2} - 3\overrightarrow {AB} .\overrightarrow {BC} + 2\overrightarrow {AB} .\overrightarrow {AC} - 6\overrightarrow {AC} .\overrightarrow {BC} \)
\( = {a^2} + \frac{{3{{\rm{a}}^2}}}{2} + {a^2} - 3{{\rm{a}}^2} = \frac{{{a^2}}}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.